题目内容
4.若y=$\frac{\sqrt{{x}^{2}-1}+\sqrt{1-{x}^{2}}}{x+1}$+7,求x+y的立方根.分析 根据二次根式有意义的条件和分式有意义的条件确定x的值,进而可得y的值,然后再计算出x+y,然后求立方根即可.
解答 解:由题意得:$\left\{\begin{array}{l}{{x}^{2}-1≥0}\\{1-{x}^{2}≥0}\\{x+1≠0}\end{array}\right.$,
解得:x=1,
则y=7,
x+y=1+7=8,
x+y的立方根为2.
点评 此题主要考查了二次根式和分式有意义的条件,以及立方根,关键是掌握分式有意义,分母不为0;二次根式的被开方数是非负数.

练习册系列答案
相关题目
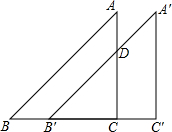 等腰直角三角形ABC中,AC=BC=10厘米,将三角形沿BC方向平移4厘米,得到等腰三角形A′B′C′,那么四边形ABB′D的面积=32平方厘米.
等腰直角三角形ABC中,AC=BC=10厘米,将三角形沿BC方向平移4厘米,得到等腰三角形A′B′C′,那么四边形ABB′D的面积=32平方厘米. 如图,已知△ABC中,AD=CD=DB,求证:∠ACB=90°.
如图,已知△ABC中,AD=CD=DB,求证:∠ACB=90°.