Question

14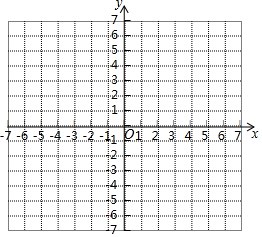．如图，在平面直角坐标系中，点A的坐标为（4，0），点B（m，n）在第四象限，点B向左平移（3m-8）（m＞$\frac{8}{3}$）个单位到达点C的位置．
（1）写出点C的坐标（用字母m、n表示）；
C（8-2m，n）．
（2）如果点C正好落在直线x=-2上，求m的值；
（3）在（2）的条件下，如果直线x=-2上有一点P，联结AP、BP，当△ABP是一个以AB为腰的等腰直角三角形时，求出此时点P的坐标．

Answer 1

分析 （1）根据平移规律填空即可；
（2）把点C的坐标代入直线x=-2上，得到关于m的方程，通过解方程求得m的值；
（3）没有指出等腰直角三角形的腰，所以需要分类讨论：AP=AB、PB=AB．利用点与坐标的性质，两点间的距离公式解答即可．

解答 解：（1）点C的纵坐标与点B的纵坐标相同，都是n，横坐标为：m-（3m-8）=8-2m，则C（8-2m，n）；
故答案是：（8-2m，n）；

（2）因为点C落在直线x=-2上，
所以-2m+8=-2，
得m=5；

（3）①当AP=AB，那么∠A=90°，如图，

易证△APH≌△BAG，
所以PH=AG=1，BG=AH=6
P（-2，-1），
②当PB=AB，那么∠B=90°，如图，

易证△AGB≌△BHP，
所以BG=PH=7，BH=AG=1，
所以P（-2，-8）．
综上所述，符合条件的点P的坐标是（-2，-1）或（-2，-8）．

点评 本题考查了一次函数综合题，需要掌握全等三角形的判定与性质，点的坐标与图形的性质，等腰三角形的性质，解题时，利用了“数形结合”、“分类讨论”等数学思想，难度中档．