题目内容
已知
，求代数式a2+b的立方根．
解：∵
、
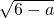有意义，
∴
，
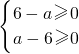解得：a=6，
∴b=28，
∴a2+b=62+28=64，
．
则代数式a2+b的立方根为4．
分析：根据二次根式有意义的条件可得出a，继而代入可得出b，然后代入代数式求立方根即可．
点评：本题考查了立方根的知识，属于基础题，关键是根据二次根式有意义的条件求出a的值．
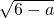、有意义，∴
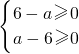，解得：a=6，
∴b=28，
∴a2+b=62+28=64，
．则代数式a2+b的立方根为4．
分析：根据二次根式有意义的条件可得出a，继而代入可得出b，然后代入代数式求立方根即可．
点评：本题考查了立方根的知识，属于基础题，关键是根据二次根式有意义的条件求出a的值．
练习册系列答案
名校课堂系列答案
相关题目
，求代数式a2-b2的值．
，求代数式[（a+b）2（a-b）2+4a2b2]÷（a2+b2）的值．
，求代数式a2-b2的值．