题目内容
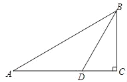
【题目】如图,在![]() 中,
中,![]() ,过点
,过点![]() 的直线
的直线![]() ,
,![]() 为
为![]() 边上一点,过点
边上一点,过点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)当![]() 为
为![]() 的中点时,四边形
的中点时,四边形![]() 是什么特殊四边形?请说明你的理由;
是什么特殊四边形?请说明你的理由;
(3)若![]() 为
为![]() 的中点,则当
的中点,则当![]() 的大小满足什么条件时,四边形
的大小满足什么条件时,四边形![]() 是正方形?请说明你的理由.
是正方形?请说明你的理由.
【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】
(1)先求出四边形ADEC是平行四边形,根据平行四边形的性质推出即可;
(2)由AD=BD,AD=CE,得到BD=CE,利用MN∥AB,得到四边形BECD是平行四边形,然后根据![]() ,即可得到四边形BECD是菱形;
,即可得到四边形BECD是菱形;
(3)根据∠A=45°,∠ACB=90°,则得到∠ABC=∠A=45°,从而得到AC=BC,即△ABC是等腰直角三角形,由D是AB中点,得到CD⊥AB,即可得到四边形BECD是正方形.
证明:(1)∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,即
,即![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() .
.
(2)四边形![]() 是菱形.理由如下:
是菱形.理由如下:
∵![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴四边形![]() 是平行四边形.
是平行四边形.
又∵![]() ,
,
∴四边形![]() 是菱形.
是菱形.
(3)当![]() 时,四边形
时,四边形![]() 是正方形,理由如下:
是正方形,理由如下:
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
由(2)知四边形![]() 是菱形,
是菱形,
∴四边形![]() 是正方形.
是正方形.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
【题目】重百超市对出售A、B两种商品开展春节促销活动,活动方案有如下两种:(同一种商品不可同时参与两种活动)
商品 | A | B | |
标价(单位:元) | 120 | 150 | |
方案一 | 每件商品出售价格 | 按标价降价30% | 按标价降价a% |
方案二 | 若所购商品达到或超过101件(不同商品可累计)时,每件商品按标价降价20%后出售 | ||
(1)某单位购买A商品50件,B商品40件,共花费9600元,试求a的值;
(2)在(1)的条件下,若某单位购买A商品x件(x为正整数),购买B商品的件数比A商品件数的2倍还多一件,请问该单位该如何选择才能获得最大优惠?请说明理由.