题目内容
已知:如图所示,等腰梯形ABCD中,AD∥BC,BD平分∠ABC.
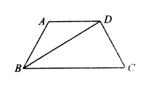
(1)求证:AB=AD;
(2)若AD=6,∠C=60°,求梯形ABCD的周长.
解:(1)证明:∵AD// BC,
∴∠ADB = ∠DBC.
∵BD平分∠ABC,
∴∠DBC=∠ABD,
∴∠ADB=∠ABD.
∴AB=AD,
(2) ∵AD//BC,AB=CD,
∴∠ABC=∠C= 60°,∠DBC= ∠ABC=30°.
∠ABC=30°.
∴∠BDC= 180°-∠DBC-∠C= 90°
∴CD= BC
BC
∴BC= 2CD
∵AD=6,
∴AB=AD= 6,
∴CD=AB=6
∴BC=12
故梯形周长为:AB+BC+CD+AD=6+12+6+6=30。
∴∠ADB = ∠DBC.
∵BD平分∠ABC,
∴∠DBC=∠ABD,
∴∠ADB=∠ABD.
∴AB=AD,
(2) ∵AD//BC,AB=CD,
∴∠ABC=∠C= 60°,∠DBC=
 ∠ABC=30°.
∠ABC=30°. ∴∠BDC= 180°-∠DBC-∠C= 90°
∴CD=
 BC
BC∴BC= 2CD
∵AD=6,
∴AB=AD= 6,
∴CD=AB=6
∴BC=12
故梯形周长为:AB+BC+CD+AD=6+12+6+6=30。

练习册系列答案
相关题目
 已知:如图所示,等腰梯形ABCD中,AB∥CD,AD=BC=4,DC=3,△ADE≌△ECB,
已知:如图所示,等腰梯形ABCD中,AB∥CD,AD=BC=4,DC=3,△ADE≌△ECB,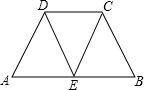 已知:如图所示,等腰梯形ABCD中,AB∥CD,AD=BC=4,DC=3,△ADE≌△ECB,
已知:如图所示,等腰梯形ABCD中,AB∥CD,AD=BC=4,DC=3,△ADE≌△ECB,