题目内容
 如图,AB=DC,AD=CB,在DA、BC的延长线上各任取一点E、F,连接E、F,求证:∠E=∠F.
如图,AB=DC,AD=CB,在DA、BC的延长线上各任取一点E、F,连接E、F,求证:∠E=∠F.考点:全等三角形的判定与性质
专题:证明题
分析:先证明四边形ABCD为平行四边形,得出AD∥BC,根据平行线的性质,可得出∠E=∠F.
解答:证明:∵AB=DC,AD=CB,
∴四边形ABCD为平行四边形(两组对边分别相等的四边形是平行四边形),
∴AD∥BC(平行四边形的对边平行),
∴∠E=∠F(两直线平行,内错角相等).
∴四边形ABCD为平行四边形(两组对边分别相等的四边形是平行四边形),
∴AD∥BC(平行四边形的对边平行),
∴∠E=∠F(两直线平行,内错角相等).
点评:本题考查了平行四边形的判定和性质,熟知平行四边形的判定是证明此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
根据下列表格的对应值
判断方程一元二次方程ax2+bx+c=0(a≠0,a、b、c为常数)一个解的范围是( )
| x | … | 3.3 | 3.4 | 3.5 | 3.6 | … |
| y=ax2+bx+c | … | -0.6 | -0.2 | 0.3 | 0.9 | … |
| A、3<x<3.3 |
| B、3.3<x<3.4 |
| C、3.4<x<3.5 |
| D、3.5<x<3.6 |
 平行四边形一边长为10,那么它的对角线长度和可以为( )
平行四边形一边长为10,那么它的对角线长度和可以为( )| A、8和12 | B、20和30 |
| C、6和8 | D、4和6 |
 知观察所A的标高(当水位为0m时的高度)为443.74m,当时水位为+3.74m,求观察所A到船只B的水平距离BC(精确到1m)
知观察所A的标高(当水位为0m时的高度)为443.74m,当时水位为+3.74m,求观察所A到船只B的水平距离BC(精确到1m)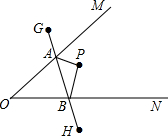 如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点,若GH的长为10cm,求△PAB的周长为
如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H,GH分别交OM、ON于A、B点,若GH的长为10cm,求△PAB的周长为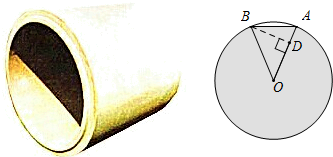
 如图,已知AB是半圆O的直径,∠BAC=32°,D是弧AC的中点,求∠DAC的度数.
如图,已知AB是半圆O的直径,∠BAC=32°,D是弧AC的中点,求∠DAC的度数.