Question

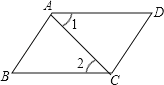
【题目】如图，已知正方形ABCD的边长是2，点E是AB边上一动点（点E与点A、B不重合），过点E作FG⊥DE交BC边于点F、交DA的延长线于点G，且FH∥AB．

（1）当DE＝时，求AE的长；

（2）求证：DE＝GF；

（3）连结DF，设AE＝x，△DFG的面积为y，求y与x之间的函数关系式．

Answer 1

【答案】（1）；（2）见解析；（3）y＝（0＜x＜2）．

【解析】

（1）根据勾股定理计算AE的长；

（2）证明△FHG≌△DAE即可解决问题；

（3）由（1）可知DE=FG，所以△DGF的底与高可以利用勾股定理用含x的式子表示出来，所以解析式就可以表示出来.

（1）∵四边形ABCD是正方形，

∴∠DAE＝90°，

∵AD＝2，DE＝，

∴AE＝＝＝；

（2）证明：∵在正方形ABCD中，∠DAE＝∠B＝90°，

∴四边形ABFH是矩形，

∴FH＝AB＝DA，

∵DE⊥FG，

∴∠G＝90°﹣∠ADE＝∠DEA，

又∴∠DAE＝∠FHG＝90°，

∴△FHG≌△DAE（AAS），

∴DE＝GF．

（3）∵△FHG≌△DAE

∴FG＝DE＝＝，

∵S△DGF＝FGDE，

∴y＝，

∴解析式为：y＝（0＜x＜2）．