题目内容
 如图AD是∠BAC的角平分线,AD的垂直平分线交BC的延长线于F,若
如图AD是∠BAC的角平分线,AD的垂直平分线交BC的延长线于F,若| AC |
| AB |
| 3 |
| 5 |
| CF |
| BF |
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:连接AF,由FE是AD的垂直平分线得到FA=FD,再根据等边对等角得到∠FAD=∠FDA,而∠BAF=∠FAD+∠1,∠ACF=∠FDA+∠2,其中由AD是∠BAC的平分线可以得到∠1=∠2,得到△BAF∽△ACF,再根据相似三角形的性质就可以得出题目结论.
解答: 解:连接AF,
解:连接AF,
∵AD是∠BAC的平分线,
∴∠1=∠2,
∵FO是AD的垂直平分线,
∴FA=FD(线段垂直平分线上的点到线段两端的距离相等),
∴∠FAD=∠FDA(等角对等边),
∵∠BAF=∠FAD+∠1,∠ACF=∠FDA+∠2,
∴∠BAF=∠ACF.
∴△BAF∽△ACF
∴AC:AB=CF:AF=AF:BF=3:5
∴AF=
BF,CF=
AF=
(
BF)=
BF
即
=
.
故选C.
 解:连接AF,
解:连接AF,∵AD是∠BAC的平分线,
∴∠1=∠2,
∵FO是AD的垂直平分线,
∴FA=FD(线段垂直平分线上的点到线段两端的距离相等),
∴∠FAD=∠FDA(等角对等边),
∵∠BAF=∠FAD+∠1,∠ACF=∠FDA+∠2,
∴∠BAF=∠ACF.
∴△BAF∽△ACF
∴AC:AB=CF:AF=AF:BF=3:5
∴AF=
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 3 |
| 5 |
| 9 |
| 25 |
即
| CF |
| BF |
| 9 |
| 25 |
故选C.
点评:本题考查了相似三角形的判定和性质,利用了角平分线的性质、线段的垂直平分线性质、等腰三角形的性质等知识,有一点难度.

练习册系列答案
相关题目
 7、如图,△ABC中,AB=AC,AD是∠BAC的平分线,DE⊥AB,DF⊥AC,问∠BDE与∠CDF是否相等?为什么?
7、如图,△ABC中,AB=AC,AD是∠BAC的平分线,DE⊥AB,DF⊥AC,问∠BDE与∠CDF是否相等?为什么?
 如图AD是∠BAC的角平分线,AD的垂直平分线交BC的延长线于F,若
如图AD是∠BAC的角平分线,AD的垂直平分线交BC的延长线于F,若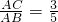 ,则
,则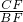 =
=



 ,则
,则 =( )
=( )



