题目内容
三角形三边长分别为a、b、c,它的三条中位线组成一个新的三角形,新的三角形的三条中位线又组成一个三角形,以此类推,第5次组成的三角形的周长是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:三角形中位线定理
专题:规律型
分析:根据三角形中位线定理,新三角形与原三角形相似,相似比是1:2,即后一个三角形的周长都是前一个三角形周长的
,以此类推,第五次组成的三角形的周长.
| 1 |
| 2 |
解答:解:由△ABC三边长为a、b、c,三条中位线组成一个新的三角形,
可知新三角形与原三角形相似,相似比是1:2,
即:后一个三角形的周长都是前一个三角形周长的,
以此类推,第n次组成的三角形的周长.
,
那么第五次组成的三角形的周长为
=
.
故选C.
可知新三角形与原三角形相似,相似比是1:2,
即:后一个三角形的周长都是前一个三角形周长的,
以此类推,第n次组成的三角形的周长.
| a+b+c |
| 2n |
那么第五次组成的三角形的周长为
| a+b+c |
| 25 |
| a+b+c |
| 32 |
故选C.
点评:此题主要考查学生对三角形中位线定理、相似三角形的判定与性质的理解与掌握.

练习册系列答案
相关题目
下列计算正确的是( )
| A、-5+4=-9 |
| B、-8-8=0 |
| C、23=6 |
| D、-42=-16 |
α,β是方程x2+2x-5=0的两个实数根,则α2+2α+αβ的值为( )
| A、5 | B、-5 | C、0 | D、10 |
下列图形中具有不稳定性的是( )
| A、长方形 | B、等腰三角形 |
| C、直角三角形 | D、锐角三角形 |
 如图,小正方形的边长为1,图中的线段AB的长度为
如图,小正方形的边长为1,图中的线段AB的长度为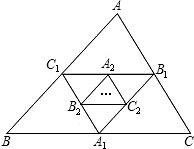 如图,A1、B1、C1分别是BC、AC、AB的中点,A2、B2、C2分别是B1C1、A1C1、A1B1的中点,…,这样延续下去,已知△ABC的周长是32,△A1B1C1的周长是l1,△A2B2C2的周长是l2,…,△A4B4C4的周长是l4,则l4=
如图,A1、B1、C1分别是BC、AC、AB的中点,A2、B2、C2分别是B1C1、A1C1、A1B1的中点,…,这样延续下去,已知△ABC的周长是32,△A1B1C1的周长是l1,△A2B2C2的周长是l2,…,△A4B4C4的周长是l4,则l4=