Question

【题目】如图，点D、E、F分别为△ABC各边中点，下列说法正确的是（　　）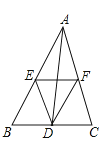

A.DE=DF
B.EF=?AB
C.S△ABD=S△ACD
D.AD平分∠BAC

Answer 1

【答案】C
【解析】解：A、∵点D、E、F分别为△ABC各边中点，
∴DE=AC，DF=AB，
∵AC≠AB，
∴DE≠DF，故该选项错误；
B、由A选项的思路可知，B选项错误、
C、∵S△ABD=BDh，S△ACD=CDh，BD=CD，
∴S△ABD=S△ACD ， 故该选项正确；
D、∵BD=CD，AB≠AC，
∴AD不平分∠BAC，
故选C．
【考点精析】解答此题的关键在于理解三角形中位线定理的相关知识，掌握连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半．