题目内容
 已知?ABCD,AB⊥AC,E在AD边上,连接BE、AC交于点F,∠ABE=∠CAD,tan∠EBC=
已知?ABCD,AB⊥AC,E在AD边上,连接BE、AC交于点F,∠ABE=∠CAD,tan∠EBC=| 1 |
| 2 |
| 5 |
考点:圆的综合题
专题:综合题
分析:过点F、B、C作⊙O,CG为⊙的直径,连接OB,GF交于H,如图,由平行四边形的性质得AD∥BC,则∠6=∠5,由于∠1=∠6,所以∠1=∠5,再根据圆周角定理得到∠2=∠G,根据等腰三角形的性质得∠3=∠4,则∠1+∠2+∠3=∠5+∠4+∠G,再利用圆周角定理由CG为直径得到∠5+∠4+∠G=90°,所以∠1+∠2+∠3=90°,易证得四边形ABHF为矩形,于是有∠BHF=90°,AF=BH,根据垂径定理由OH⊥GF得到GH=FH,所以OH为△GFC的中位线,得到OH=
FC=
(
+1),
在Rt△CFG中,利用正切的定义可计算出FG=2(
+1),再利用勾股定理计算出CG=5+
,则OB=
CG=
(5+
),然后可计算出BH=OB-OH=2,于是得到AF=2.
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
在Rt△CFG中,利用正切的定义可计算出FG=2(
| 5 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
解答:解:过点F、B、C作⊙O,CG为⊙的直径,连接OB,GF交于H,如图,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠6=∠5,
而∠1=∠6,
∴∠1=∠5,
∵∠2=∠G,∠3=∠4,
∴∠1+∠2+∠3=∠5+∠4+∠G,
∵CG为直径,
∴∠GFC=90°,
∴∠5+∠4+∠G=90°,
∴∠1+∠2+∠3=90°,
而AB⊥AC,
∴∠BAC=90°,
∴四边形ABHF为矩形,
∴∠BHF=90°,AF=BH,
∴OH⊥GF,
∴GH=FH,
∴OH为△GFC的中位线,
∴OH=
FC=
(
+1),
在Rt△CFG中,tan∠G=tan∠2=
=
,
∴FG=2(
+1),
∴CG=
=5+
,
∴OB=
CG=
(5+
),
∴BH=OB-OH=
(5+
)-
(
+1)=2,
∴AF=2.
故答案为2.

∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠6=∠5,
而∠1=∠6,
∴∠1=∠5,
∵∠2=∠G,∠3=∠4,
∴∠1+∠2+∠3=∠5+∠4+∠G,
∵CG为直径,
∴∠GFC=90°,
∴∠5+∠4+∠G=90°,
∴∠1+∠2+∠3=90°,
而AB⊥AC,
∴∠BAC=90°,
∴四边形ABHF为矩形,
∴∠BHF=90°,AF=BH,
∴OH⊥GF,
∴GH=FH,
∴OH为△GFC的中位线,
∴OH=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
在Rt△CFG中,tan∠G=tan∠2=
| 1 |
| 2 |
| FC |
| FG |
∴FG=2(
| 5 |
∴CG=
| FG2+CF2 |
| 5 |
∴OB=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
∴BH=OB-OH=
| 1 |
| 2 |
| 5 |
| 1 |
| 2 |
| 5 |
∴AF=2.
故答案为2.
点评:本题考查了圆的综合题:熟练掌握圆周角定理、垂径定理、平行四边形的性质和矩形的判定与性质;会运用勾股定理和锐角三角函数的定义进行几何计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在实数-
,0,
,π,
中,无理数有( )个.
| 2 |
| 3 |
| 5 |
| 4 |
| A、1 | B、2 | C、3 | D、4 |
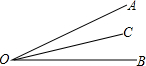 如图,下列结论中,不能说明射线OC平分∠AOB的是( )
如图,下列结论中,不能说明射线OC平分∠AOB的是( )| A、∠AOC=∠BOC |
| B、∠AOB=2∠BOC |
| C、∠AOB=2∠BOC |
| D、∠AOC+∠BOC=∠BOA |
