题目内容
如图，C、D、E将线段AB分成1：2：3：4四部分，M、P、Q、N分别是AC、CD、DE、EB的中点，MN=15cm，求PQ的长．
解：设AC=x，则CD=2x，DE=3x，EB=4x，
∵M、N分别是AC、EB的中点，
∴MC=
x，EN=2x，
∴MN=MC+CD+DE+EN=x+2x+3x+2x=
x，
而MN=15cm，
∴x=15cm，解得x=2cm，
∵P、Q分别是CD、DE的中点，
∴PD=x，DQ=
x，
∴PQ=PD+DQ=x+x=
x=×2xm=5cm．
分析：设AC=x，根据题意有CD=2x，DE=3x，EB=4x，由M、N分别是AC、EB的中点得到MC=x，EN=2x，则MN=MC+CD+DE+EN=x=15，于是可计算出x=2，再由P、Q分别是CD、DE的中点得PD=x，DQ=x，然后利用PQ=PD+DQ=x+x=x进行计算．
点评：本题考查了两点间的距离：连接两点间的线段的长度叫两点间的距离．
∵M、N分别是AC、EB的中点，
∴MC=
x，EN=2x，∴MN=MC+CD+DE+EN=
x+2x+3x+2x=x，而MN=15cm，
∴
x=15cm，解得x=2cm，∵P、Q分别是CD、DE的中点，
∴PD=x，DQ=
x，∴PQ=PD+DQ=x+
x=x=×2xm=5cm．分析：设AC=x，根据题意有CD=2x，DE=3x，EB=4x，由M、N分别是AC、EB的中点得到MC=
x，EN=2x，则MN=MC+CD+DE+EN=x=15，于是可计算出x=2，再由P、Q分别是CD、DE的中点得PD=x，DQ=x，然后利用PQ=PD+DQ=x+x=x进行计算．点评：本题考查了两点间的距离：连接两点间的线段的长度叫两点间的距离．
练习册系列答案
相关题目
26、如图，AD是∠CAB的角平分线，DE∥AB，DF∥AC，EF交AD于点O．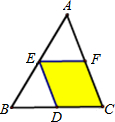
16、如图，EF是△ABC的中位线，将△AEF沿AB方向平移到△EBD的位置，点D在BC上，已知△AEF的面积为5，则图中阴影部分的面积为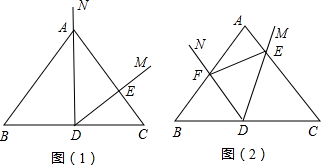
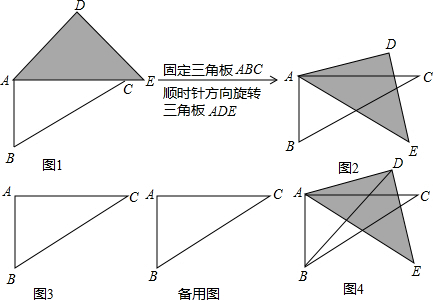
8、如图，在直角坐标系中，网格线是由若干个边长为1的小正方形拼成的．△ABC与△A'B'C'的顶点都是小正方形的顶点．若将△ABC平移后得到△A'B'C'，则正确的平移方法是（ ）