��Ŀ����
��ͼ�٣���ƽ��ֱ�������У���A������Ϊ��1����2������B������Ϊ��3����1�������κ���y=��x2��ͼ��Ϊl1��
��1��ƽ��������l1��ʹƽ�ƺ�������߾�����A����������B��
������������ĺ�������ʽ�� ����
��д������ƽ���Ҿ���A�Ľ���ʽ ��
��2��ƽ��������l1��ʹƽ�ƺ�������߾���A��B���㣬���õ�������l2����ͼ�ڣ���������l2�ĺ�������ʽ������C�����꣬�����ABC�������
��3����y�����Ƿ���ڵ�P��ʹS��ABC=S��ABP�������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�

��1������������y=��x2��1����2��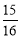 ����3�����ڣ���P������Ϊ��0��
����3�����ڣ���P������Ϊ��0��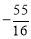 ����0��
����0��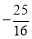 ����
����
��������
�����������1���ٸ���ʵ���������ֱ��д�������
����ƽ���Ժ�Ķ��κ�������ʽ�ǣ�y=��x2+c���ѣ�1����2�����뼴�����c=��1���Ӷ��õ������Ľ���ʽ��y=��x2��1��
��2�����ô���ϵ����������ú����Ľ���ʽ����Ϊ����ʽ�õ���C �����꣬����A��B��C����ֱ���x��Ĵ��ߣ�����ֱ�ΪD��EE��F����á�ABC�������
��3���ֵ���Pλ�ڵ�G���·����Ϸ��������������������⣮
�����������������
��1����������
��y=��x2��1��
��2����l2�Ľ���ʽ��y=x2+bx+c��
��l2������A��1����2����B��3����1����
��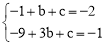 ����ã�
����ã�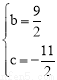 ��
��
��l2�Ľ���ʽ�ǣ� ��
��
��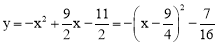 ��
��
�ඥ��C��������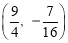 ��
��
���ͼ1������A��B��C����ֱ���x��Ĵ��ߣ�����ֱ�ΪD��E��F��
��AD=2��CF=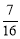 ��BE=1��DE=2��DF=
��BE=1��DE=2��DF=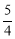 ��FE=
��FE=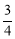 ��
��
��S��ABC=S����ABED��S����BCFE��S����ACFD=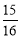 ��
��
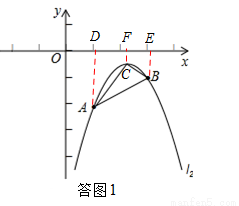
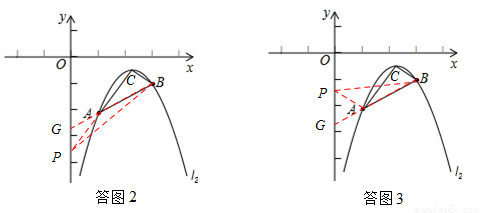
��3�����ڣ����ͼ2��3���ӳ�BA��y���ڵ�G��
��ֱ��AB�Ľ���ʽΪ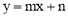 ��
��
��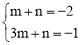 �����
�����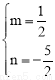 ��
��
��ֱ��AB�Ľ���ʽΪ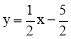 ��
��
���G��������0��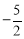 ����
����
���P��������0��h����
�ٵ���Pλ�ڵ�G���·�ʱ�����ͼ2��PG=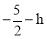 ������AP��BP��
������AP��BP��
��S��ABP=S��BPG��S��APG=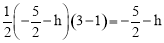 ��
��
�֡�S��ABC=S��ABP=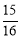 ����h=
����h=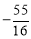 ��
��
���P��������0��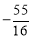 ����
����
�ڵ���Pλ�ڵ�G���Ϸ�ʱ�����ͼ3��PG=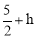 ��
��
ͬ�Ͽɵ�h=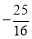 ����P������Ϊ��0��
����P��������0��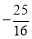 ����
����
���������������P��������0��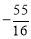 ����0��
����0��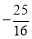 ����
����
���㣺1�����κ����ۺ��⣻2���߶�ƽ�����⣻3������ϵ������Ӧ�ã�4�������ϵ�������뷽�̵Ĺ�ϵ��5�����κ��������ʣ�6�������κ����������7������˼�롢ת��˼��ͷ���˼���Ӧ�ã�



 �ĸ�Ϊ ��
�ĸ�Ϊ �� B��
B�� C��
C�� D��
D��
