Question

【题目】在正方形ABCD中，P为AB边上一点，将△BCP沿CP折叠，得到△FCP．

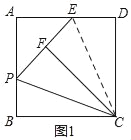
（1）如图1，延长PF交AD于E，求证：EF=ED；

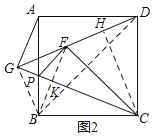
（2）如图2，DF，CP的延长线交于点G，求的值．

Answer 1

【答案】（1）证明见解析（2）

【解析】

（1）连接CE，通过全等三角形的判定，得到Rt△CFE≌Rt△CDE，进而得出结论；

（2）连接BG、BF、BD，作CH⊥DF，垂足为H．依据△CFG≌△CBG，可得GF=GB，进而得出△GBF是等腰直角三角形，故BF＝BG．再判定△BGA∽△FBD，即可得到．

（1）如图1，连接CE，

∵四边形ABCD是正方形，

∴BC=CD，∠B=∠D=90°．

∵△PBC和△FPC关于PC对称，

∴BC=CF，∠B=∠PFC=90°．

∴∠EFC=90°．

∴∠EFC=∠D=90°，CF=CD．

∵CE=CE，

∴Rt△EFC≌Rt△DFC（HL）．

∴EF=ED．

（2）如图2，连接BG、BF、BD，作CH⊥DF，垂足为H．

∵四边形ABCD是正方形，

∴BC=CD．

∵CH⊥DF，

∴∠HCF=，

∵△PBC和△FPC关于PC对称，

∴BC=CF，∠FCG=∠BCG．

∴EB⊥CG．

又∵CG=CG，

∴△CFG≌△CBG．

∴GF=GB．

∵∠HCF=，∠FCG=∠BCG=，

∴∠HCK==45°．

∴∠PFH=135°．

∴∠GFB=45°．

∴∠GBF=45°．

∴△GBF是等腰直角三角形．

∴．

∵∠ABD=45°，

∴∠GBA=∠FBD．

∵，

∴△BGA∽△FBD．

∴．