题目内容
10.水果市场某批发商用2500元购进某种水果进行试销,由于销售状况良好,批发商又调拨6000元资金购进同种水果,但这次进货价比上次每千克少0.5元,且购进的量是上次的3倍.(1)试销时该水果的进货价每千克多少元?
(2)批发商按每千克4元的定价出售,当售出大部分后余下600千克时,问水果至多按几折出售完,批发商在这两次水果销售中共获利不少于6300元?
分析 (1)设试销时该水果的进货价每千克x元,根据这次进货价比上次每千克少0.5元,购进该水果的数量是上次的3倍,可列方程求解.
(2)设余下600千克水果至多按a折出售完,批发商在这两次水果销售中共获利不少于6300元,列出不等式求解即可.
解答 解:(1)设试销时该水果进货价为x元/千克,则:
$\frac{2500}{x}$×3=$\frac{6000}{x-0.5}$,
解得:x=2.5,
经检验x=2.5是方程的解,且符合题意.
答:试销时该水果的进货价每千克2.5元.
(2)由(1)知:第一次购进水果$\frac{2500}{2.5}$=1000千克,第二次购进水果3000千克,
设余下600千克水果至多按a折出售完,批发商在这两次水果销售中共获利不少于6300元,则:
(1000+3000-600)×4+600×4×$\frac{a}{10}$-(2500+6000)≥6300,
解得:a≥5.
答:余下600千克水果至多按5折出售完,批发商在这两次水果销售中共获利才不少于6300元.
点评 本题考查分式方程的应用,理解题意的能力,关键是根据这次进货价比上次每千克少0.5元,购进苹果的数量是上次的3倍,列出方程求出每千克多少元,然后求出总千克数,从而求出解.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
20.下列运算正确的是( )
| A. | 2x-x=1 | B. | (x2)3=x5 | C. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{2}$ | D. | 20=0 |
1.一种细胞的直径约为0.000052米,将0.000052用科学记数法表示为( )
| A. | 5.2×105 | B. | 5.2×10-5 | C. | 5.2×10-4 | D. | 52×10-6 |
18.关于x的一元二次方程x2+4x+k=0有两个实数根,则k的取值范围是( )
| A. | k≤-4 | B. | k≥-4 | C. | k≤4 | D. | k>4 |
5.2016年普宁市重点项目累计完成投资187.35亿元,将187.35亿用科学记数法表示为( )
| A. | 187.35×108 | B. | 1.8735×109 | C. | 1.8735×1010 | D. | 1.8735×1011 |
15.如果二次根式$\sqrt{x-2}$有意义,那么x的取值范围是( )
| A. | x>2 | B. | x≥2 | C. | x≠2 | D. | x≤2 |
2.某个密码锁的密码由三个数字组成,每个数字都是0-9这十个数字中的一个,只有当三个数字与所设定的密码及顺序完全相同时,才能将锁打开.如果仅忘记了锁设密码的最后那个数字,那么一次就能打开该密码的概率是( )
| A. | $\frac{1}{9}$ | B. | $\frac{1}{10}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
19.如图是由棱长为1的正方体搭成的某几何体三视图,则图中棱长为1的正方体的个数是( )


| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
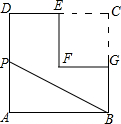 如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致为( )
如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致为( )