��Ŀ����
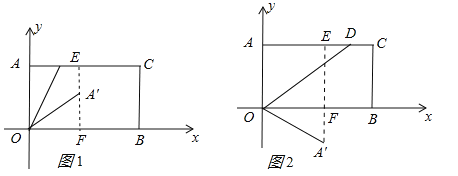
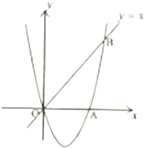
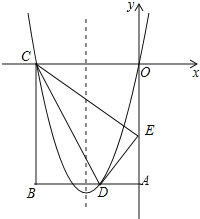
����Ŀ����ͼ���ھ���OABC�У�OA��5��AB��4����DΪ��AB��һ�㣬����BCD��ֱ��CD�۵���ʹ��Bǡ�����ڱ�OA�ϵĵ�E�����ֱ���OC��OA���ڵ�ֱ��Ϊx�ᣬy�Ὠ��ƽ��ֱ������ϵ��
��1����OE�ij�������O��D��C���������ߵĽ���ʽ��
��2��һ����P�ӵ�C��������CB��ÿ��2����λ���ȵ��ٶ����B�˶���ͬʱ����Q��E���������EC��ÿ��1����λ���ȵ��ٶ����C�˶�������P�����Bʱ������ͬʱֹͣ�˶������˶�ʱ��Ϊt�룬��tΪ��ֵʱ��DP��DQ��
��3������N�ڣ�1���������ߵĶԳ����ϣ���M���������ϣ��Ƿ���������ĵ�M���N��ʹM��N��C��EΪ������ı�����ƽ���ı��Σ������ڣ������M�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��OE��3��y��![]() x2+
x2+![]() x����2��t��
x����2��t��![]() ����3���������������ĵ�M��������Ϊ��2��16����6��16����2����
����3���������������ĵ�M��������Ϊ��2��16����6��16����2����![]() ����
����
��������
��1�����۵������ʿ����CE��CO����Rt��COE�У��ɹ��ɶ��������OE����AD��m����Rt��ADE�У��ɹ��ɶ��������m��ֵ�������D�����꣬���C��O���㣬���ô���ϵ��������������߽���ʽ��
��2����t��ʾ��CP��BP�ij�����֤����DBP�ա�DEQ���ɵõ�BP��EQ�������t��ֵ��
��3�������N�����꣬�����������ENΪ�Խ��ߣ���EMΪ�Խ��ߣ���ECΪ�Խ��ߣ�����ƽ���ı��ε����ʿ���öԽ��ߵĽ�������꣬�Ӷ������M��ĺ����꣬�ٴ��������߽���ʽ�����M������꣮
��1����CE��CB��5��CO��AB��4��
����Rt��COE��OE��![]() ��
��![]() ��3��
��3��
��AD��m����DE��BD��4��m��
��OE��3��
��AE��5��3��2��
��Rt��ADE�У��ɹ��ɶ����ɵ�AD2+AE2��DE2����m2+22����4��m��2�����m��![]() ��
��
��D����![]() ����5����
����5����
��C����4��0����O��0��0����
�����O��D��C�����������Ϊy��ax��x+4����
�ੁ5����![]() a����
a����![]() +4�������a��
+4�������a��![]() ��
��
�������߽���ʽΪy��![]() x��x+4����
x��x+4����![]() x2+
x2+![]() x��
x��
��2����CP��2t��
��BP��5��2t��
��BD��![]() ��DE��
��DE��![]() ��
��![]() ��
��
��BD��DE��
��Rt��DBP��Rt��DEQ��
![]() ��
��
��Rt��DBP��Rt��DEQ��HL����
��BP��EQ��
��5��2t��t��
��t��![]() ��
��
��3���������ߵĶԳ���Ϊֱ��x����2��
����N����2��n����
���������֪C����4��0����E��0����3����
��M��m��y����
�ٵ�ENΪ�Խ��ߣ����ı���ECNM��ƽ���ı���ʱ��
���߶�EN���е������Ϊ![]() ���߶�CM�е������Ϊ
���߶�CM�е������Ϊ![]() ��
��
��EN��CM����ƽ�֣�
��![]() ����1�����m��2��
����1�����m��2��
��M�����������ϣ�
��y��![]() ��22+
��22+![]() ��2��16��
��2��16��
��M��2��16����
�ڵ�EMΪ�Խ��ߣ����ı���ECMN��ƽ���ı���ʱ��
���߶�EM���е������Ϊ![]() ���߶�CN�е������Ϊ
���߶�CN�е������Ϊ![]() ��
��
��EM��CN����ƽ�֣�
��![]() ����3�����m����6��
����3�����m����6��
�֡�M�����������ϣ�
��y��![]() ������6��2+
������6��2+![]() ������6����16��
������6����16��
��M����6��16����
�۵�CEΪ�Խ��ߣ����ı���EMCN��ƽ���ı���ʱ��
��MΪ�����ߵĶ��㣬��M����2����![]() ����
����
���Ͽ�֪���������������ĵ�M��������Ϊ��2��16����6��16����2����![]() ����
����

 Сѧ���AB��ϵ�д�
Сѧ���AB��ϵ�д� ABC����ȫ�ž�ϵ�д�
ABC����ȫ�ž�ϵ�д�����Ŀ��ijС��![]() ��¥�������ۣ���֪
��¥�������ۣ���֪![]() ��¥ij��Ԫ��
��¥ij��Ԫ��![]() �㣬һ¥Ϊ���̣�ֻ�ⲻ�ۣ���¥���ϼ۸����£���
�㣬һ¥Ϊ���̣�ֻ�ⲻ�ۣ���¥���ϼ۸����£���![]() ���ۼ�Ϊ
���ۼ�Ϊ![]() Ԫ/��
Ԫ/��![]() ���ӵ�
���ӵ�![]() ����ÿ����һ�㣬ÿƽ�����ۼ����
����ÿ����һ�㣬ÿƽ�����ۼ����![]() Ԫ����֮ÿ��һ�㣬ÿƽ�����ۼ۽���
Ԫ����֮ÿ��һ�㣬ÿƽ�����ۼ۽���![]() Ԫ����֪�õ�Ԫÿ�������Ϊ
Ԫ����֪�õ�Ԫÿ�������Ϊ![]() ��
��![]()
�Żݻ
�һ����һ���Ը������з������![]() ������
������![]() ����ҵ�ѹ�
����ҵ�ѹ�![]() Ԫ��
Ԫ��
�������������һ���Ը������з������![]() �������ͣ�
�������ͣ�
��1�������±��У����������ۼ�![]() (Ԫ/��
(Ԫ/��![]() )��¥��
)��¥��![]() (
(![]() ȡ������)֮��ĵ�����ϵʽ��
ȡ������)֮��ĵ�����ϵʽ��
¥�� |
|
|
|
|
�ۼ� | ���� |
|
��2��ij�ͻ��빺��õ�Ԫ��![]() ���һ��¥��������һ���Ը��幺������Բμ���ͼ�Żݻ��������������������Żݷ���������
���һ��¥��������һ���Ը��幺������Բμ���ͼ�Żݻ��������������������Żݷ���������