��Ŀ����
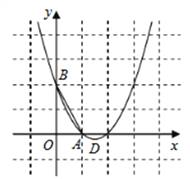
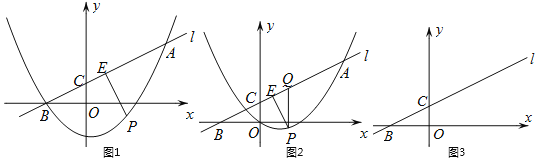
����Ŀ����ͼ1��������C1��y��![]() x2+ax+b��ֱ��l���ڵ�A(8��6)��B(��4��0)��ֱ��l��y����C����P��ֱ��l�·���������C1��һ���㣨����A��B���ص㣩��PE��AB�ڵ�E�����P�ĺ�����Ϊm��
x2+ax+b��ֱ��l���ڵ�A(8��6)��B(��4��0)��ֱ��l��y����C����P��ֱ��l�·���������C1��һ���㣨����A��B���ص㣩��PE��AB�ڵ�E�����P�ĺ�����Ϊm��
��1����������C1��ֱ��l�Ľ���ʽ��
��2����AB��3PE����m��ֵ��
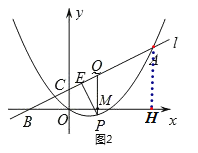
��3��������C1����ƽ��t����λ���õ�������C2����PΪ������C2��һ�㣬����x���·���PE��AB�ڵ�E������P��x��Ĵ��߽�x���ڵ�M����ֱ��l�ڵ�Q��
����ͼ2����t��4ʱ�����PQE�ܳ������ֵ��
�ڵ���P��������C2���˶�ʱ���߶�PM��QM��ֵ�ڲ��ϱ仯����![]() �����ֵΪ1�����ʱt���� ����ֱ��д���������
�����ֵΪ1�����ʱt���� ����ֱ��д���������
���𰸡���1��![]() �� y��
�� y��![]() x+2����2��m��2
x+2����2��m��2![]() ����3����8+
����3����8+![]() ����
����![]()
��������
��1������A��B���������y��![]() x2+ax+b��������������ߵĽ���ʽ����A��B�������y��mx+n���������ֱ��l�Ľ���ʽ��
x2+ax+b��������������ߵĽ���ʽ����A��B�������y��mx+n���������ֱ��l�Ľ���ʽ��
��2����ͼ1����A��AH��x�ᣬPF��x�ᣬEF��x�ύPF��F������ABH�ס�EPF����AB��3PE�����PF��4��EF��2�����P(m��![]() m2��
m2��![]() m��
m��![]() )����E(m��2��
)����E(m��2��![]() m2��
m2��![]() m+
m+![]() )����E����ֱ��l�Ľ���ʽ�������m��ֵ��
)����E����ֱ��l�Ľ���ʽ�������m��ֵ��
��3������t��4ʱ��ƽ�ƺ�Ľ���ʽC2Ϊ��y��![]() x2��
x2��![]() x����P(m��
x����P(m��![]() m2��
m2��![]() m)����Q(m��
m)����Q(m��![]() m+2)�����PQ�����ֵ����һ�����������PQE���ܳ����ֵ������д��ƽ�ƺ�Ľ���ʽ�����ú�m��t�Ĵ���ʽ��ʾ��PM��MQ�ij�����
m+2)�����PQ�����ֵ����һ�����������PQE���ܳ����ֵ������д��ƽ�ƺ�Ľ���ʽ�����ú�m��t�Ĵ���ʽ��ʾ��PM��MQ�ij�����![]() ��1���г�����ʽ���������ɺ�����ͼ���������t��ֵ��
��1���г�����ʽ���������ɺ�����ͼ���������t��ֵ��
�⣺��1������A��8��6����B����4��0�����룬
�ã�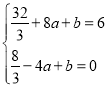 ��
��
��ã� ��
��
�������߽���ʽΪy��![]() x2��
x2��![]() x��
x��![]() ��
��
��ֱ��l�Ľ���ʽΪy��mx+n��
��A��B������룬�ã�![]() ��
��
��� ��
��
��ֱ��l�Ľ���ʽΪy��![]() x+2��
x+2��
��2����ͼ1����A��AH��x�ᣬPF��x�ᣬEF��x�ύPF��F��
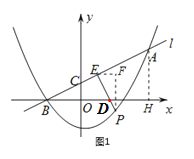
�ߡ�CBO+��BDE=90�㣬��P+��PDH=90�㣬
���CBD=��P��
�֡ߡ�F=��AHB=90�㣬
���ABH�ס�EPF��
��AB��3PE��
��BH��3PF��AH��3EF��
��BH��12��AH��6��
��PF��4��EF��2��
��P(m��![]() m2��
m2��![]() m��
m��![]() )����E(m��2��
)����E(m��2��![]() m2��
m2��![]() m+
m+![]() )��
)��
��E����ֱ��l����ã�m2��4m��2��0��
���m��2![]() ��
��
��3����A��AH��x����H��
����y��![]() x2��
x2��![]() x��
x��![]() =
=![]() ��
��
�൱t��4ʱ��ƽ�ƺ�Ľ���ʽC2Ϊ��y=![]() ��
��![]() x2��
x2��![]() x��
x��
��P(m��![]() m2��
m2��![]() m)����Q(m��
m)����Q(m��![]() m+2)��
m+2)��
��PQ��-![]() m2+2m+2����
m2+2m+2����![]() (m��6)2+8��
(m��6)2+8��
����m��6ʱ��PQȡ���ֵ8��
�ߡ�ABH=��EPQ����AHB=��PEQ��
����PQE�ס�ABH��
��EQ��PE��PQ��1��2��![]() ��
��
���PQE���ܳ����ֵ��PQ+PE+EQ��8+2��![]() +
+![]() ��8+
��8+![]() ��
��
����y��=![]() ��
��
��ƽ�ƺ�Ľ���ʽΪ��y��![]() x2��
x2��![]() +
+![]() ��
��
��PM����![]() m2+
m2+![]() ��
��![]() ��MQ��
��MQ��![]() m+2��
m+2��![]() ��1��
��1��
��-![]() m2+
m2+![]() ��
��![]() ��0��
��0��
����m����![]() ��t��1ʱ��-
��t��1ʱ��-![]() m2+
m2+![]() ��
��![]() �����ֵ0��
�����ֵ0��
��m��t��1����-![]() m2+
m2+![]() ��
��![]() ��0��
��0��
���t��![]() ��
��
�ʴ�Ϊ��![]() ��
��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�