Question

【题目】（题文）如图，已知抛物线经过，两点，顶点为.

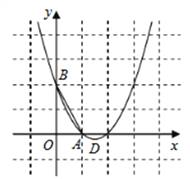
（1）求抛物线的解析式；

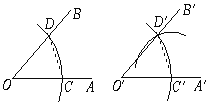
（2）将绕点顺时针旋转后，点落在点的位置，将抛物线沿轴平移后经过点，求平移后所得图象的函数关系式；

（3）设（2）中平移后，所得抛物线与轴的交点为，顶点为，若点在平移后的抛物线上，且满足的面积是面积的2倍，求点的坐标.

Answer 1

【答案】（1）抛物线的解析式为.（2）平移后的抛物线解析式为：.（3）点的坐标为或.

【解析】（1）利用待定系数法，将点A，B的坐标代入解析式即可求得；

（2）根据旋转的知识可得：A（1，0），B（0，2），∴OA=1，OB=2，

可得旋转后C点的坐标为（3，1），当x=3时，由y=x2-3x+2得y=2，可知抛物线y=x2-3x+2过点（3，2）∴将原抛物线沿y轴向下平移1个单位后过点C．∴平移后的抛物线解析式为：y=x2-3x+1；

（3）首先求得B1，D1的坐标，根据图形分别求得即可，要注意利用方程思想．

详解: （1）已知抛物线经过,,

∴，解得，

∴所求抛物线的解析式为.

（2）∵,，∴，，

可得旋转后点的坐标为.

当时，由得，

可知抛物线过点.

∴将原抛物线沿轴向下平移1个单位长度后过点.

∴平移后的抛物线解析式为：.

（3）∵点在上，可设点坐标为，

将配方得，∴其对称轴为.由题得Ｂ１（0,1）．

①当时，如图①，

∵，

∴，

∴，

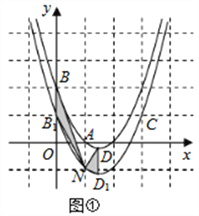
此时，

∴点的坐标为.

②当时，如图②，

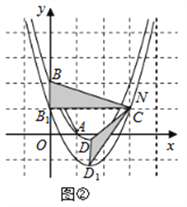
同理可得，

∴，

此时，

∴点的坐标为.

综上，点的坐标为或.