Question

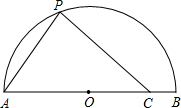（2013•太仓市二模）如图，点P在半径为5的半圆上运动，AB是⊙O直径，OC=3，当△ACP是等腰三角形时，点P到AB的距离是

2

6

或4.8

．

Answer 1

分析：分两种情况考虑：当AP=CP时，如图1所示，过P作PQ垂直于AB，求出PQ的长，即为P到AB的距离；当AP=AC时，连接PB，由AB为圆O的直径，利用直径所对的圆周角为直角得到三角形APB为直角三角形，利用勾股定理求出PB的长，利用面积法求出PQ的长，即为P到AB的距离．

解答：解：分两种情况考虑：
（1）当AP=CP时，如图1所示，
过P作PQ⊥AB，可得AQ=CQ=4，
∴在Rt△PQO中，OP=5，OQ=5-4=1，
则根据勾股定理得：PQ=

52-12

=2

6

，即点P到AB的距离是2

6

；
（2）当AP=AC时，如图2所示，过P作PQ⊥AB，连接BP，由AB为圆O的直径，得到∠APB=90°，
在Rt△APB中，AB=10，AP=AC=8，根据勾股定理得：PB=6，
∵S_△APB=

1

2

×AP×PB=

1

2

×AB×PQ，
∴PQ=

AP•BP

AB

=4.8，即点P到AB的距离是4.8，
综上，点P到AB的距离是2

6

或4.8．
故答案为：2

6

或4.8．

点评：此题考查了垂径定理，勾股定理，利用了分类讨论的思想，熟练掌握垂径定理是解本题的关键．