题目内容
如图,已知A1,A2,A3,…,An是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1,A2,A3,…,An+1作x轴的垂线交一次函数 x的图象于点B1,B2,B3,…,Bn+1,连接A1B2,B1A2,A2B3,B2A3,…,AnBn+1,BnAn+1依次产生交点P1,P2,P3,…,Pn,则Pn的横坐标是 .
x的图象于点B1,B2,B3,…,Bn+1,连接A1B2,B1A2,A2B3,B2A3,…,AnBn+1,BnAn+1依次产生交点P1,P2,P3,…,Pn,则Pn的横坐标是 .
【答案】分析:因为B1、B2、B3、B4、B5、B6、B7、B8的横坐标为1,2,3,4,5;
代入函数 x可得B1、B2、B3、B4、B5的纵坐标为
x可得B1、B2、B3、B4、B5的纵坐标为 、1、
、1、 、2、
、2、 .于是作P1C⊥x轴,P2D⊥x轴,P3E⊥x轴,于是A1C:A2C=A1B1:A2B2=
.于是作P1C⊥x轴,P2D⊥x轴,P3E⊥x轴,于是A1C:A2C=A1B1:A2B2= :1,又A1A2=1,所以A1C=
:1,又A1A2=1,所以A1C= ,
,
同理可得A2D= ,A3E=
,A3E= ,于是OC=1+
,于是OC=1+ ,OD=2+
,OD=2+ ,OE=3+
,OE=3+ …,Pn的横坐标为:n+
…,Pn的横坐标为:n+ .
.
解答:解:Pn的横坐标为:n+ .
.

点评:此题是一道探索性题目,考查了一次函数的性质、平行线分线段成比例定理等知识.
通过计算得出P1P2P3各点横坐标,分析数的特点,总结出规律,便可求出Pn点的坐标.
代入函数
 x可得B1、B2、B3、B4、B5的纵坐标为
x可得B1、B2、B3、B4、B5的纵坐标为 、1、
、1、 、2、
、2、 .于是作P1C⊥x轴,P2D⊥x轴,P3E⊥x轴,于是A1C:A2C=A1B1:A2B2=
.于是作P1C⊥x轴,P2D⊥x轴,P3E⊥x轴,于是A1C:A2C=A1B1:A2B2= :1,又A1A2=1,所以A1C=
:1,又A1A2=1,所以A1C= ,
,同理可得A2D=
 ,A3E=
,A3E= ,于是OC=1+
,于是OC=1+ ,OD=2+
,OD=2+ ,OE=3+
,OE=3+ …,Pn的横坐标为:n+
…,Pn的横坐标为:n+ .
.解答:解:Pn的横坐标为:n+
 .
.
点评:此题是一道探索性题目,考查了一次函数的性质、平行线分线段成比例定理等知识.
通过计算得出P1P2P3各点横坐标,分析数的特点,总结出规律,便可求出Pn点的坐标.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

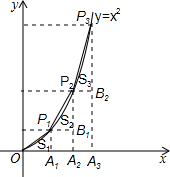 如图,已知A1,A2,A3,…,A2009是x轴上的点,且OA1=A1A2=A2A3=…=A2008A2009=1,分别过点A1,A2,A3,…,A2009作x轴的垂线交二次函数y=x2(x≥0)的图象于点P1,P2,P3,…,P2009,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…,依次进行下去,最后记△P2008B2008P2009的面积为S2009,则S2009-S2008=
如图,已知A1,A2,A3,…,A2009是x轴上的点,且OA1=A1A2=A2A3=…=A2008A2009=1,分别过点A1,A2,A3,…,A2009作x轴的垂线交二次函数y=x2(x≥0)的图象于点P1,P2,P3,…,P2009,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…,依次进行下去,最后记△P2008B2008P2009的面积为S2009,则S2009-S2008= 如图,已知A1,A2,A3,…,A2006是x轴上的点,且OA1=A1A2=A2A3=…=A2005A2006=1,分别过点A1,A2,A3,…,A2006作x轴的垂线交二次函数y=x2(x≥0)的图象于点P1,P2,P3,…,P2006点,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…,依次进行下去,最后记△P2005B2005P2006的面积为S2006,则S2006-S2005=
如图,已知A1,A2,A3,…,A2006是x轴上的点,且OA1=A1A2=A2A3=…=A2005A2006=1,分别过点A1,A2,A3,…,A2006作x轴的垂线交二次函数y=x2(x≥0)的图象于点P1,P2,P3,…,P2006点,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…,依次进行下去,最后记△P2005B2005P2006的面积为S2006,则S2006-S2005=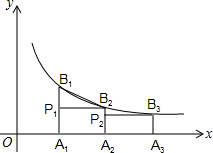 如图,已知A1,A2,A3,…An是x轴上的点,且OA1=A1A2=A2A3=…=An-1An=1,分别过点A1,A2,A3,…An作x轴的垂线交反比例函数y=
如图,已知A1,A2,A3,…An是x轴上的点,且OA1=A1A2=A2A3=…=An-1An=1,分别过点A1,A2,A3,…An作x轴的垂线交反比例函数y= 如图,已知A1,A2,A3,…,A2012是x轴上的点,且0A1=A1A2=A2A3=…=A2010A2011=A2011A2012=1,分别过点A1,A2,A3,…,A2012作x轴的垂线交二次函数y=x2(x≥0)的图象于点P1,P2,P3,…,P2012,若△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…依次进行下去,最后记△P2011B2011P2012的面积为S20121,则
如图,已知A1,A2,A3,…,A2012是x轴上的点,且0A1=A1A2=A2A3=…=A2010A2011=A2011A2012=1,分别过点A1,A2,A3,…,A2012作x轴的垂线交二次函数y=x2(x≥0)的图象于点P1,P2,P3,…,P2012,若△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3,…依次进行下去,最后记△P2011B2011P2012的面积为S20121,则