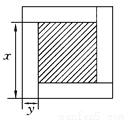
��Ŀ����
������������ȷ���ǣ� ��
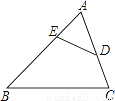
��ȫ�������ζ�Ӧ����ȣ��������Ƕ�Ӧ��ȵ�����������ȫ�ȣ������߶�Ӧ��ȵ���������ȫ�ȣ��������߶�Ӧ��ȵ���������ȫ�ȡ�
A. 4�� B. 3�� C. 2�� D. 1��
C ����������������ȫ�ȵ����ʿ�֪����ȷ�� �ڸ���ȫ�������ε��ж�������֪AAA������Ϊ�ж����������Ǵ��� �����߶�Ӧ��ȵ��������Σ�����SSS��ȫ�ȣ�������ȷ�� �������߶�Ӧ��ȵ��������Σ��������������ж���������ȫ�ȣ����Ǵ��� ��ѡC��
��ϰ��ϵ�д�
 ѧ���쳵�����ּ��������ҵ�½����������ϵ�д�
ѧ���쳵�����ּ��������ҵ�½����������ϵ�д� �����ѧСѧ�꼶�νӵ������㽭��ѧ������ϵ�д�
�����ѧСѧ�꼶�νӵ������㽭��ѧ������ϵ�д� Сѧ�����ҵ���ϴ�ѧ������ϵ�д�
Сѧ�����ҵ���ϴ�ѧ������ϵ�д� ���Ž�����ٰθ��νӹ㶫���������ϵ�д�
���Ž�����ٰθ��νӹ㶫���������ϵ�д� �����������ҵ�������������ϵ�д�
�����������ҵ�������������ϵ�д�
�����Ŀ
�±������˴���ʽ��x2+bx+c��x��һЩ��Ӧֵ��
x | �� | ��2 | ��1 | 0 | 1 | 2 | 3 | �� |
��x2+bx+c | �� | 5 | n | c | 2 | ��3 | ��10 | �� |
��1�����ݱ����е����ݣ�ȷ��b��c��n��ֵ��
��2����y=��x2+bx+c��ֱ��д��0��x��2ʱy�����ֵ.
��1��b=-2��c=5��n=6����2��y�����ֵ��5�� �������������������1���ѣ���2��0������1��2���ֱ���멁x2+bx+c�еõ�����b��c�ķ����飬Ȼ��ⷽ���鼴�ɵõ�b��c��ֵ��Ȼ�����x=��1ʱ�Ĵ���ʽ��ֵ���ɵõ�n��ֵ�� ��2�����ñ������ݼ�����⣮ �����������1�����ݱ������ݿɵ� ����ã� �ੁx2+bx+c=��x2��2x+5�� ��x=��1ʱ����x2...

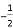 �ĵ����ǣ� ��
�ĵ����ǣ� �� B. -2 C. 2 D.
B. -2 C. 2 D. 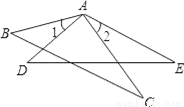
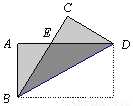
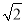 x+sin��=0��������ȵ�ʵ����������Ǧ����ڣ� ��
x+sin��=0��������ȵ�ʵ����������Ǧ����ڣ� ��