题目内容
我市某化工厂现有甲种原料290kg,乙种原料212kg,计划利用这两种原料生产A,B两种产品共80件.生产一件A产品需要甲种原料5kg,乙种原料 1.5kg,生产成本是120元;生产一件B产品,需要甲种原料2.5kg,乙种原料3.5kg,生产成本是200元.
1.5kg,生产成本是120元;生产一件B产品,需要甲种原料2.5kg,乙种原料3.5kg,生产成本是200元.
(1)该化工厂现有的原料能否保证生产?若能的话,有几种生产方案,请你设计出来;
(2)设生产A,B两种产品的总成本为y元,其中一种的生产件数为x,试写出y与x之间的函数关系,并利用函数的性质说明(1)中哪种生产方案总成本最低?最低生产总成本是多少?
(1)设安排生产A种产品x件,则生产B种产品(80-x)件,依题意得……(2分)
 解得34≤x≤36.……………………………(6分)
解得34≤x≤36.……………………………(6分)
因为x为整数,所以x只能取34或35或36.
该工厂现有的原料能保证生产,有三种生产方案:
方案一:生产A种产品34件,B种产品46件;
方案二:生产A种产品35件,B种产品45件;
方案三:生产A种产品36件,B种产品44件…………………(8分)
(2)设生产A种产品x件,则生产B种产品(80-x)件,
y与x的关系为: y=120x+200(80-x),
即y=-80x+16000(x=34,35,36)………(10分)
因为y随x的增大而减小,所以x取最大值时,y有最小值.
当x=36时,y的最小值是
y=-80×36+16000=13120.
即第三种方案总成本最低,最低生产成本是13120元

练习册系列答案
相关题目
 ,
, 
 )的图象不经过第三象限,那么m的取值范围是
)的图象不经过第三象限,那么m的取值范围是  中,自变量x的取值范围是( )
中,自变量x的取值范围是( ) ,并写出该不等式组的整数解.
,并写出该不等式组的整数解.
 在实数范围内有意义,则
在实数范围内有意义,则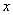 的取值范围是 .
的取值范围是 .