Question

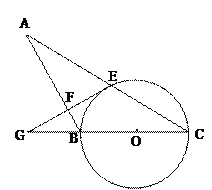
【题目】如图，在△ABC中，以BC为直径的⊙O交AC于点E，过点E作EF⊥AB于点F，延长EF交CB的延长线于点G，且∠ABG=2∠C．

（1）求证：EF是⊙O的切线；

（2）若，⊙O的半径是3，求AF的长．

Answer 1

【答案】（1）证明见解析（2）

【解析】分析：（1）连接EO，由∠EOG=2∠C、∠ABG=2∠C知∠EOG=∠ABG，从而得AB∥EO，根据EF⊥AB得EF⊥OE，即可得证；

（2）由∠ABG=2∠C、∠ABG=∠C+∠A知∠A=∠C，即BA=BC=6，在Rt△OEG中求得OG==5、BG=OG-OB=2，在Rt△FGB中求得BF=BGsin∠EGO，根据AF=AB-BF可得答案．

详解：（1）如图，连接EO，则OE=OC，

∴∠EOG=2∠C，

∵∠ABG=2∠C，

∴∠EOG=∠ABG，

∴AB∥EO，

∵EF⊥AB，

∴EF⊥OE，

又∵OE是⊙O的半径，

∴EF是⊙O的切线；

（2）∵∠ABG=2∠C，∠ABG=∠C+∠A，

∴∠A=∠C，

∴BA=BC=6，

在Rt△OEG中，∵sin∠EGO=，

∴OG=，

∴BG=OG﹣OB=2，

在Rt△FGB中，∵sin∠EGO=，

∴BF=BGsin∠EGO=2×，

则AF=AB﹣BF=6﹣．