题目内容
如图,已知二次函数 的图象与
的图象与 轴交于A、B两点,与
轴交于A、B两点,与 轴交于点P,顶点为C(1,-2).
轴交于点P,顶点为C(1,-2).
(1)求此函数的关系式;
(2)作点C关于 轴的对称点D,顺次连接A、C、B、D.若在抛物线上存在点E,使直线PE将四边形ABCD分成面积相等的两个四边形,求点E的坐标;
轴的对称点D,顺次连接A、C、B、D.若在抛物线上存在点E,使直线PE将四边形ABCD分成面积相等的两个四边形,求点E的坐标;
(3)在(2)的条件下,抛物线上是否存在一点F,使得△PEF是以P为直角顶点的直角三角形?若存在,求出点F的坐标及△PEF的面积;若不存在,请说明理由.
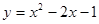 ;E(3,2) ;3
;E(3,2) ;3
解析试题分析:1)∵ 的顶点为C(1,-2),
的顶点为C(1,-2),
∴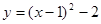 ,
,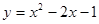 . 2
. 2
2)设直线PE对应的函数关系式为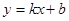 .由题意,四边形ACBD是菱形.
.由题意,四边形ACBD是菱形.
故直线PE必过菱形ACBD的对称中心M. 1
由P(0,-1),M(1,0),得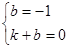 .从而
.从而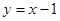 , 2
, 2
设E( ,
,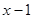 ),代入
),代入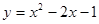 ,得
,得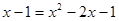 .
.
解之得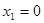 ,
,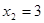 ,根据题意,得点E(3,2) 2
,根据题意,得点E(3,2) 2
3)假设存在这样的点F,可设F( ,
,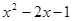 ).过点F作FG⊥
).过点F作FG⊥ 轴,垂足为点G.
轴,垂足为点G.
在Rt△POM和Rt△FGP中,∵∠OMP+∠OPM=90°,∠FPG+∠OPM=90°,
∴∠OMP=∠FPG,又∠POM=∠PGF,∴△POM∽△FGP.
∴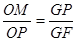 .又OM=1,OP=1,∴GP=GF,即
.又OM=1,OP=1,∴GP=GF,即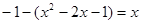 .
.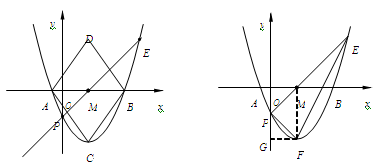
解得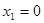 ,
,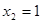 ,根据题意,
,根据题意,
得F(1,-2).
故点F(1,-2)即为所求. 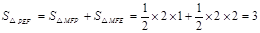
考点:相似三角形的判定
点评:解答本题的的关键是熟练掌握有两组角对应相等的两个三角形相似;两组边对应成比例且夹角相等的三角形相似.

练习册系列答案
相关题目
 的一个动点,过点P作x轴的垂线,垂足为D(m,0),并与直线OA交于点C.
的一个动点,过点P作x轴的垂线,垂足为D(m,0),并与直线OA交于点C. (2013•呼和浩特)如图,已知二次函数的图象经过点A(6,0)、B(-2,0)和点C(0,-8).
(2013•呼和浩特)如图,已知二次函数的图象经过点A(6,0)、B(-2,0)和点C(0,-8).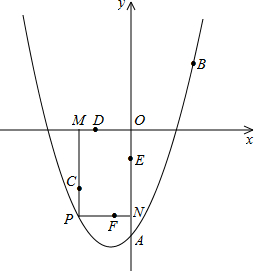 (2013•常德)如图,已知二次函数的图象过点A(0,-3),B(
(2013•常德)如图,已知二次函数的图象过点A(0,-3),B( 如图,已知二次函数的图象与x轴交于A(2,0)、B(6,0)两点,与y轴交于点D(0,4).
如图,已知二次函数的图象与x轴交于A(2,0)、B(6,0)两点,与y轴交于点D(0,4). 如图,已知二次函数的图象(0≤x≤3.4),关于该函数在所给自变量的取值范围内,下列说法正确的是( )
如图,已知二次函数的图象(0≤x≤3.4),关于该函数在所给自变量的取值范围内,下列说法正确的是( )