题目内容
【题目】如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点P在AB上,AP=2,点E、F同时从点P出发,分别沿PA、PB以每秒1个单位长度的速度向点A、B匀速运动,点E到达点A后立刻以原速度沿AB向点B运动,点F运动到点B时停止,点E也随之停止.在点E、F运动过程中,以EF为边作正方形EFGH,使它与△ABC在线段AB的同侧.设E、F运动的时间为t/秒(t>0),正方形EFGH与△ABC重叠部分面积为S.
(1)当t=1时,正方形EFGH的边长是 . 当t=3时,正方形EFGH的边长是 .
(2)当0<t≤2时,求S与t的函数关系式;
(3)直接答出:在整个运动过程中,当t为何值时,S最大?最大面积是多少? 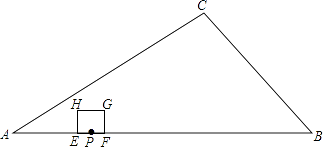
【答案】
(1)2;4
(2)解:
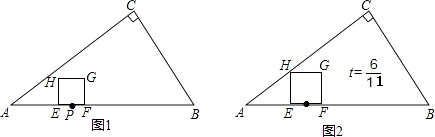 ,
,
如图1,EP=FP=t,HE=EF=2t,
如图2,EP=FP=t,HE=EF=2t,
AE=AP﹣EP=2﹣t,
由 ![]() =
= ![]() ,即
,即 ![]() =
= ![]() 得t=
得t= ![]() ,
,
故S重叠面积=S正方形=(2t)2=4t2(0<t≤ ![]() ),
),
如图4,AE=AP﹣EP=2﹣t,
LE= ![]() AE=
AE= ![]() ,
,
HL=HE﹣LE=2t﹣ ![]() (2﹣t),
(2﹣t),
HM= ![]() HL=
HL= ![]() [2t﹣
[2t﹣ ![]() (2﹣t)],
(2﹣t)],
由HG= ![]() HL,即2t=
HL,即2t= ![]() [2t﹣
[2t﹣ ![]() (2﹣t)]
(2﹣t)]
解得:t= ![]() ,
,
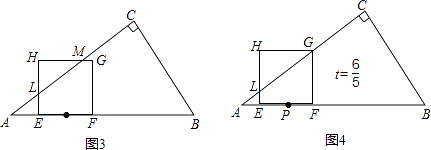
如图3,AE=AP﹣EP=2﹣t,
LE= ![]() AE=
AE= ![]() ,
,
HL=HE﹣LE=2t﹣ ![]() (2﹣t),
(2﹣t),
HM= ![]() HL=
HL= ![]() [2t﹣
[2t﹣ ![]() (2﹣t)],
(2﹣t)],
S重叠面积=S正方形﹣S△HLM=EF2﹣ ![]() HL×HM=﹣
HL×HM=﹣ ![]() t2+
t2+ ![]() t﹣
t﹣ ![]() (
( ![]() <t≤
<t≤ ![]() );
);
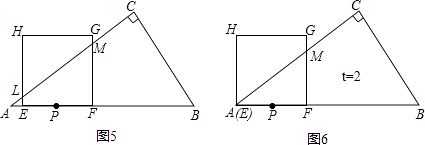
如图5,AE=AP﹣EP=2﹣t,LE= ![]() AE=
AE= ![]() (2﹣t),MF=
(2﹣t),MF= ![]() AF=
AF= ![]() (2+t),
(2+t),
S重叠面积=S梯形LEFM= ![]() (EL+MF)×EF=3t(
(EL+MF)×EF=3t( ![]() <t≤2)
<t≤2)
(3)解:由(2)知:当0<t≤ ![]() 时,
时,
S与t的函数关系式是S=2t×2t=4t2= ![]() ;
;
当 ![]() <t≤
<t≤ ![]() 时,
时,
S与t的函数关系式是:
S=﹣ ![]() t2+
t2+ ![]() t﹣
t﹣ ![]() =
= ![]() ;
;
当 ![]() <t≤2时;
<t≤2时;
S与t的函数关系式是:
S=3t=6;
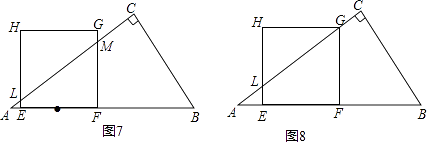
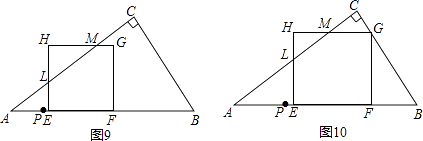
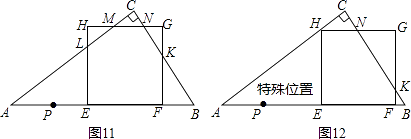
当t>2时,观察正方形与三角形的重叠面积随t值变化情况,容易得到只有当 ![]() ≤t≤
≤t≤ ![]() 时,S才有可能取到最大值.如图7,图8,图9,图10,图11,图12,
时,S才有可能取到最大值.如图7,图8,图9,图10,图11,图12,
显然,图10,图12是图11的特殊情况,只要算出图11的重叠面积关于t的函数关系式,即可得出在图11中,
由PA+AE=t,得AE=t﹣2,FB=AB﹣AE﹣EF=10﹣(t﹣2)﹣4=8﹣t,
由LE= ![]() E=
E= ![]() (t﹣2),HL=HE﹣LE=4﹣
(t﹣2),HL=HE﹣LE=4﹣ ![]() (t﹣2),HM=
(t﹣2),HM= ![]() HL=
HL= ![]() [4﹣
[4﹣ ![]() (t﹣2)]
(t﹣2)]
得S△HLM= ![]() HL×HM=
HL×HM= ![]() [4﹣
[4﹣ ![]() (t﹣2)]×
(t﹣2)]× ![]() [4﹣
[4﹣ ![]() (t﹣2)]
(t﹣2)]
由FB=AB﹣AE﹣EF=10﹣(t﹣2)﹣4=8﹣t,则FK= ![]() (8﹣t),GK=GF﹣KF=4﹣
(8﹣t),GK=GF﹣KF=4﹣ ![]() (8﹣t),
(8﹣t),
由NG= ![]() GK=
GK= ![]() [4﹣
[4﹣ ![]() (8﹣t)],
(8﹣t)],
则S△NGK= ![]() GK×NG=
GK×NG= ![]() [4﹣
[4﹣ ![]() (8﹣t)]×
(8﹣t)]× ![]() [4﹣
[4﹣ ![]() (8﹣t)],
(8﹣t)],
S重叠面积=16﹣S△NCK﹣S△HLM═﹣ ![]() t2+
t2+ ![]() t﹣
t﹣ ![]() ,
,
=﹣ ![]() (t﹣
(t﹣ ![]() )2+
)2+ ![]()
∴综上所述,当t= ![]() 时S有最大值,为
时S有最大值,为 ![]() .
.
由图形知,在整个过程中,S取得最大值只会在图11中产生,故当t= ![]() 时S有最大值,为
时S有最大值,为
【解析】解:(1)当时t=1时,则PE=1,PF=1, ∴正方形EFGH的边长是2;
当t=3时,PE=1,PF=3,
∴正方形EFGH的边长是4.
所以答案是:2,4;
【考点精析】根据题目的已知条件,利用二次函数的最值和勾股定理的概念的相关知识可以得到问题的答案,需要掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案