题目内容
已知:sinα-cosα=
,则sinαcosα=
(0<α<90°)
| 1 |
| 4 |
| 15 |
| 32 |
| 15 |
| 32 |
分析:对sinα-cosα=
两边平方,然后根据sin2α+cos2α=1即可求解.
| 1 |
| 4 |
解答:解:∵sinα-cosα=
,
∴(sinα-cosα)2=
,
∴sin2α-2sinαcosα+cos2α=
,
∵sin2α+cos2α=1
∴2sinαcosα=1-
=
.
∴sinαcosα=
.
| 1 |
| 4 |
∴(sinα-cosα)2=
| 1 |
| 16 |
∴sin2α-2sinαcosα+cos2α=
| 1 |
| 16 |
∵sin2α+cos2α=1
∴2sinαcosα=1-
| 1 |
| 16 |
| 15 |
| 16 |
∴sinαcosα=
| 15 |
| 32 |
点评:本题主要考查了同角的三角函数的关系,正确理解sin2α+cos2α=1是关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
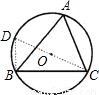
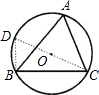 阅读材料,解答问题:
阅读材料,解答问题: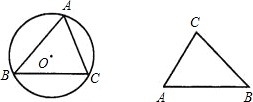
 =
= =
= =2R.
=2R. =
= ,
, ,即
,即 =2R,
=2R, =2R,
=2R, =2R,
=2R, =
= =
= =2R,
=2R, =2R,
=2R, =2R”的证明过程,请你把“
=2R”的证明过程,请你把“ =2R”的证明过程补写出来.
=2R”的证明过程补写出来. ,CA=
,CA= ,∠A=60°,求△ABC的外接圆半径R及∠C.
,∠A=60°,求△ABC的外接圆半径R及∠C.

 =
= =
= =2R.
=2R. =
= ,
, ,即
,即 =2R,
=2R, =2R,
=2R, =2R,
=2R, =
= =
= =2R,
=2R, =2R,
=2R, =2R”的证明过程,请你把“
=2R”的证明过程,请你把“ =2R”的证明过程补写出来.
=2R”的证明过程补写出来. ,CA=
,CA= ,∠A=60°,求△ABC的外接圆半径R及∠C.
,∠A=60°,求△ABC的外接圆半径R及∠C.

 =
= =
=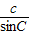 =2R.
=2R. =
= ,
, ,即
,即 =2R,
=2R, =2R,
=2R, =2R,
=2R, =
= =
= =2R,
=2R, =2R,
=2R, =2R”的证明过程,请你把“
=2R”的证明过程,请你把“ =2R”的证明过程补写出来.
=2R”的证明过程补写出来. ,CA=
,CA=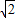 ,∠A=60°,求△ABC的外接圆半径R及∠C.
,∠A=60°,求△ABC的外接圆半径R及∠C.
 =
=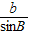 =
= =2R.
=2R. =
= ,
, ,即
,即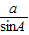 =2R,
=2R, =2R,
=2R, =2R,
=2R, =
= =
= =2R,
=2R, =2R,
=2R, =2R”的证明过程,请你把“
=2R”的证明过程,请你把“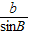 =2R”的证明过程补写出来.
=2R”的证明过程补写出来. ,CA=
,CA= ,∠A=60°,求△ABC的外接圆半径R及∠C.
,∠A=60°,求△ABC的外接圆半径R及∠C.
