Question

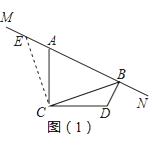
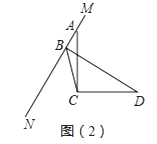
【题目】如图，已知AB∥CD，分别探究下面三个图形中∠P和∠A，∠C的关系，请你从所得三个关系中任意选出一个，说明你探究结论的正确性．

结论：（1）___________________；

（2）____________________；

（3）_____________________；

（4）选择结论____________，说明理由．

Answer 1

【答案】（1）∠APC+∠PAB+∠PCD=360°；（2）∠APC=∠PAB+∠PCD；（3）∠PCD=∠APC+∠PAB；（4）∠APC+∠PAB+∠PCD=360°，理由见解析．

【解析】

（1）过点P作PE∥AB，则AB∥PE∥CD，再根据两直线平行，同旁内角互补即可解答；

（2）过点P作PF∥AB，则AB∥CD∥PF，再根据两直线平行，内错角相等即可解答；

（3）根据AB∥CD，可得出∠1=∠PCD，再根据三角形外角的性质进行解答；

（4）选择以上结论任意一个进行证明即可．

解：（1）过点P作PE∥AB，则AB∥PE∥CD，

∴∠1+∠PAB=180°，

∠2+∠PCD=180°，

∴∠APC+∠PAB+∠PCD=360°．

故答案为：∠APC+∠PAB+∠PCD=360°；

（2）过点P作直线PF∥AB，

∵AB∥CD，

∴AB∥PF∥CD，

∴∠PAB=∠1，∠PCD=∠2，

∴∠APC=∠PAB+∠PCD．

故答案为：∠APC=∠PAB+∠PCD；

（3）∵AB∥CD，

∴∠1=∠C，

∵∠1=∠PAB+∠APC，

∴∠PCD=∠APC+∠PAB．

故答案为：∠PCD=∠APC+∠PAB．

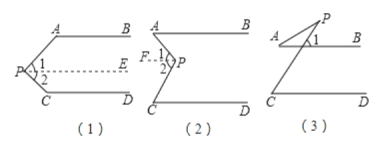
（4）选择结论∠APC+∠PAB+∠PCD=360°

理由：过点P作PE∥AB，则AB∥PE∥CD，

∴∠1+∠PAB=180°，

∠2+∠PCD=180°，

∴∠APC+∠PAB+∠PCD=360°

故答案为：∠APC+∠PAB+∠PCD=360°．