题目内容
如图矩形ABCD,AB=4,BC=10,AE、DF分别为∠DAB和∠ADC的平分线,则四边形AEFD的面积为
分析:首先根据题意证明△ABE和△DCF都是等腰三角形,从而得到AB=BE=4,CD=CF=4,进而可以求出EF的长,再利用梯形的面积公式可求出答案.
解答:解:∵四边形ABCD是矩形,
∴AD=BC=10,AB=DC=4,∠BAD=∠ADC=90°,
∵AE、DF分别为∠DAB和∠ADC的平分线,
∴∠BAE=45°,∠CDF=45°,
∴△ABE和△DCF都是等腰三角形,
∴AB=BE=4,CD=CF=4,
∴EF=10-4-4=2,
∴四边形AEFD的面积为:
(EF+AD)×AB=
(2+10)×4=24.
故答案为:24.
∴AD=BC=10,AB=DC=4,∠BAD=∠ADC=90°,
∵AE、DF分别为∠DAB和∠ADC的平分线,
∴∠BAE=45°,∠CDF=45°,
∴△ABE和△DCF都是等腰三角形,
∴AB=BE=4,CD=CF=4,
∴EF=10-4-4=2,
∴四边形AEFD的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:24.
点评:此题主要考查了矩形的性质,等腰三角形的判定,以及梯形的面积,解决此题的关键是求出EF的长.

练习册系列答案
相关题目
 如图矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E,F,AB=3,BC=4,则图中阴影部分的面积为
如图矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点E,F,AB=3,BC=4,则图中阴影部分的面积为 如图矩形ABCD中,AB=8cm,CB=4cm,E是DC的中点,BF=
如图矩形ABCD中,AB=8cm,CB=4cm,E是DC的中点,BF=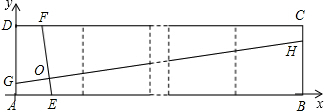
 如图矩形ABCD中,AB=1,AD=
如图矩形ABCD中,AB=1,AD=