Question

【题目】已知，在△ABC中，∠C=90°，AC=BC=7，D是AB的中点，点E在AC上，点F在BC上，DE=DF，若BF=4，则EF=_______

Answer 1

【答案】或5或

【解析】

分别就E，F在AC,BC上和延长线上，分别画出图形，过D作DG⊥AC，DH⊥BC，垂足为G，H，通过构造全等三角形和运用勾股定理作答即可.

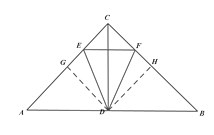
解：①过D作DG⊥AC，DH⊥BC，垂足为G，H

∴DG∥BC,∠CDG=∠CDH=45°

又∵D是AB的中点，

∴DG=BC

同理：DH=AC

又∵BC=AC

∴DG=DH

在Rt△DGE和Rt△DHF中

DG=DH,DE=DF

∴Rt△DGE≌Rt△DHF（HL）

∴GE=HF

又∵DG=DH,DC=DC

∴△GDC≌△FHC

∴CG=HC

∴CE=GC-GE=CH-HF=CF=AB-BF=3

∴EF=

②过D作DG⊥AC，DH⊥BC，垂足为G，H

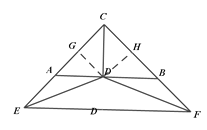
∴DG∥BC,∠CDG=∠CDH=45°

又∵D是AB的中点，

∴DG=BC

同理：DH=AC

又∵BC=AC

∴DG=DH

在Rt△DGE和Rt△DHF中

DG=DH,DE=DF

∴Rt△DGE≌Rt△DHF（HL）

∴GE=HF

又∵DG=DH,DC=DC

∴△GDC≌△FHC

∴CG=HC

∴CE=CF=AC+AE=AB+BF=7+4=11

∴EF=

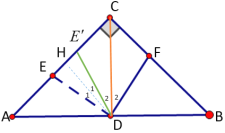
③如图，以点D为圆心，以DF长为半径画圆交AC边分别为E、，过点D作DH⊥AC于点H，可知，可证△EHD≌△，，△DHC为等腰直角三角形，

∴∠1+∠2=45°

∴∠EDF=2（∠1+∠2）=90°

∴△EDF为等腰直角三角形

可证

∴AE=CF=3,CE=BF=4

∴

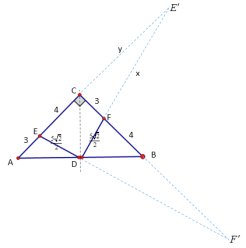
④有第③知，EF=5，且△EDF为等腰直角三角形，

∴ED=DF=,可证△,

综上可得：

∴