Question

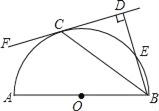
【题目】如图，AB是⊙O的直径，点C在⊙O上，CD⊥AB于D，AD=2，CD=4．∠BCD的角平分线CE与过点B的切线l交过点E．

（1）求⊙O半径的长；

（2）求点E到直线BC的距离．

Answer 1

【答案】（1）5；（2）8；

【解析】

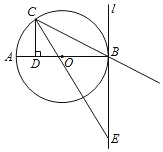
（1）如图1中，连接OC，设⊙O的半径为r．在Rt△CDO中，利用勾股定理即可解决问题．

（2）如图2中，过点E作EF⊥CD，垂足为点F，EG⊥CB，垂足为G，则∠EFD=90°，只要证明四边形BDFE是矩形，求出EF，利用角平分线的性质可得EG=EF即可解决问题．

（1）如图1中，连接OC，设⊙O的半径为r．

∵AD=2，OD=r﹣2，

∵CD⊥AB，

∴∠CDO=90°，

在Rt△CDO中，∵CD2+DO2=CO2，

∴42+（r﹣2）2=r2，

∴r=5，

⊙O的半径为5．

（2）如图2中，过点E作EF⊥CD，垂足为点F，EG⊥CB，垂足为G，则∠EFD=90°，

∵直线l切⊙O于B，

∴AB⊥l，

∴∠DBE=90°，

∵CD⊥AB，

∴∠BDF=90°，

∴四边形BDFE是矩形，

∴EF=BO+OD=8，

∵点E在∠BCD的平分线上，

∴EG=EF=8．

∴点E到直线BC的距离为8．