Question

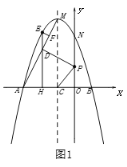
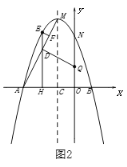
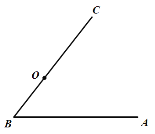
【题目】如图，点O在的边上，以为半径作，的平分线交于点D，过点D作于点E．

（1）尺规作图（不写作法，保留作图痕迹），补全图形；

（2）判断与交点的个数，并说明理由．

Answer 1

【答案】（1）见解析；（2）与有1个交点，理由见解析

【解析】

（1）根据已知圆心和半径作圆、作已知角的平分线、过直线外一点作已知直线的垂线的尺规作图的步骤作图即可；

（2）连接OD，由OB=OD，得到∠1=∠2，再由角平分线得出∠1=∠3，等量代换进而证出OD∥BA，根据两直线平行同旁内角互补，得到∠ODE=90°，由此得出OD是的切线，即与有1个交点.

解：（1）如下图，补全图形：

（2）如下图，连接OD，

∵点D在上，

∴OB=OD，

∴∠1=∠2，

又∵BM平分，

∴∠1=∠3，

∴∠2=∠3，

∴OD∥BA，

∴∠ODE+∠BED=180°，

∵

∴∠ODE=90°，

∴ED是的切线，

∴与有1个交点.