Question

以下是单位长度为1的正方形方格图，每个方格的顶点叫做格点．
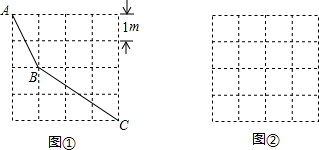
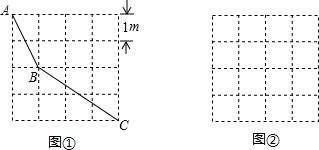
（1）如图①由边长为1m的正方形地砖铺设的地面示意图，小明沿图中所示的折线从A→B→C所走的路程为

（

5

+

13

）

m（结果保留根号）
（2）在图②中画出有一边长为

10

的一个等腰△ABC，三角形的顶点必须在格点上．

Answer 1

分析：（1）将AB与BC分别放在两个直角三角形中，分别利用勾股定理求出AB与BC，求出AB+BC即为小明沿图中所示的折线从A→B→C所走的路程长；
（2）如图所示，在直角三角形PBC中，由PB与PC的长，利用勾股定理求出BC的长，同理求出AB及AC的长，可得出AB=AC，即三角形ABC为等腰三角形，BC长为

10

，可得出△ABC为所求的三角形．

解答：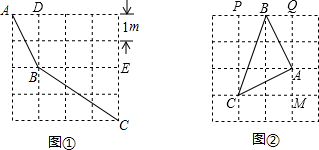
解：（1）如图所示，可得出△ADB与△BEC都为直角三角形，
在Rt△ABD中，AD=1m，BD=2m，
根据勾股定理得：AB=

AD2+DB2

=

5

m，
在Rt△BEC中，BE=3m，CE=2m，
根据勾股定理得：BC=

BE2+CE2

=

13

m，
则小明沿图中所示的折线从A→B→C所走的路程为（

5

+

13

）m；
（2）如图所示，在Rt△PBC中，PB=1，PC=3，
根据勾股定理得：BC=

PB2+PC2

=

10

，
在Rt△ABQ中，BQ=1，AQ=2，
根据勾股定理得：AB=

AQ2+BQ2

=

5

，
在Rt△ACM中，AM=1，CM=2，
根据勾股定理得：AC=

AM2+CM2

=

5

，
∴AB=AC，即△ABC为等腰三角形，
则△ABC为所求的三角形．
故答案为：（1）（

5

+

13

）

点评：此题考查了勾股定理，以及等腰三角形的性质，属于网格型试题，网格型题是近几年中考的热点试题，熟练运用勾股定理是解本题的关键．