题目内容
17.【提出问题】在等边△ABC中,点D为直线BC上的一动点(不与B,C重合),连接AD,以AD为边在AD的右侧作等边△ADE,连接CE.

(1)如图1,当点D在边BC上时,求证:∠ABC=∠ACE,AC=CE+CD;
(2)如图2,当点D在边CB的延长线上时,其它条件不变,请补全图形,结论AC=CE+CD是否成立?若成立,写出证明过程;若不成立,直接写出AC,CE,CD之间的数量关系;
【变式拓展】
如图3,△ABC为等腰三角形,AB=BC,当点D在边BC上时,连接AD,以AD为边在AD的右侧作等腰△ADE,使AD=ED,连接CE,若∠BCA=∠DEA,试探究∠ABC与∠ACE的数量关系,并说明理由.
分析 (1)可证明△BAD≌△CAE,再利用线段的和差可证得结论;
(2)可证明△ABD≌△ACE,同样可得到BD=CE,AB=AC=BC,则可得到AC=CD-CE;
(3)变式拓展:可先证明△ABC∽△ADE,可得到$\frac{BA}{DA}$=$\frac{AC}{AE}$,进一步可证明△ABD∽△ACE,可证得结论.
解答 (1)证明:∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=60°,
又∵△ADE是等边三角形,
∴AD=AE,∠DAE=60°,
∴∠BAC=∠DAE,即∠BAD+∠DAC=∠DAC+∠CAE,
∴∠BAD=∠CAE,
在△BAD和△CAE中
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$
∴△BAD≌△CAE(SAS),
∴∠ABC=∠ACE,BD=CE,
∴AC=BC=BD+CD,
即AC=CE+CD;
(2)解:图形如图所示,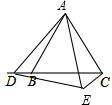
结论AC=CE+CD不成立,
数量关系为AC=CD-CE,
证明如下:
∵△ABC是等边三角形,
∴AB=AC=BC,∠BAC=60°,
又∵△ADE是等边三角形,
∴AD=AE,∠DAE=60°,
∴∠BAC=∠DAE,即∠BAD+∠BAE=∠BAE+∠CAE,
∴∠BAD=∠CAE,
在△BAD和△CAE中
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$
∴△BAD≌△CAE(SAS),
∴∠ABC=∠ACE,BD=CE,
∴AC=BC=CD-BD,
即AC=CD-CE;
(3)变式拓展:
解:∠ABC=∠ACE,
理由如下:
∵AB=AC,
∴∠BAC=∠BCA,
∵AD=DE,
∴∠DAE=∠DEA,
∵∠ACB=∠AED,
∴∠BAC=∠DAE,
∴△BAC∽△DAE,
∴$\frac{BA}{DA}$=$\frac{AC}{AE}$,
又∠BAC-∠DAC=∠DAE-∠DAC,
∴∠BAD=∠CAE,
∴△BAD∽△CAE,
∴∠ABC=∠ACE.
点评 本题为三角形综合应用,涉及知识点有等腰三角形、等边三角形的性质,全等三角形、相似三角形的判定和性质等.在(1)(2)问中在证明三角形全等时注意角相等的找法,在(3)中利用相似三角形的对应边成比例为证明三角形相似找到条件是解题的关键.本题考查知识点较多,综合性较强,难度适中.

| A. | $\frac{1}{3}$ | B. | $\frac{5}{18}$ | C. | $\frac{2}{9}$ | D. | $\frac{1}{6}$ |
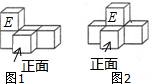 如图,图1是由5个完全相同的正方体堆成的几何体,现将标有E的正方体平移至如图2所示的位置,下列说法中正确的是( )
如图,图1是由5个完全相同的正方体堆成的几何体,现将标有E的正方体平移至如图2所示的位置,下列说法中正确的是( )| A. | 左、右两个几何体的主视图相同 | B. | 左、右两个几何体的左视图相同 | ||
| C. | 左、右两个几何体的俯视图不相同 | D. | 左、右两个几何体的三视图不相同 |
| A. | $\sqrt{-2}$ | B. | $\sqrt{0}$ | C. | $\sqrt{-(-2)}$ | D. | $\sqrt{(-1)^{2}}$ |
| A. | 4.5,2 | B. | 4,6 | C. | 4,4 | D. | 3.5,4 |
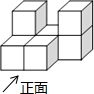 如图所示的几何体是由七个相同的小正方体组合而成的,它的左视图是( )
如图所示的几何体是由七个相同的小正方体组合而成的,它的左视图是( )



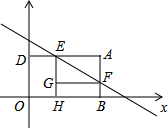 如图,矩形ABOD的两边OB,OD都在坐标轴的正半轴上,OD=4,另两边与一次函数y=-2x+b的图象分别相交于点E,F,且DE=2,过点E作EH⊥轴于点H,过点F作FG⊥EH于点G.
如图,矩形ABOD的两边OB,OD都在坐标轴的正半轴上,OD=4,另两边与一次函数y=-2x+b的图象分别相交于点E,F,且DE=2,过点E作EH⊥轴于点H,过点F作FG⊥EH于点G.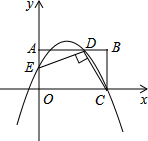 如图,平面直角坐标系xOy中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=2,OC=3,AD=2,连接DC,过点D作DE⊥DC交OA于点E.
如图,平面直角坐标系xOy中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=2,OC=3,AD=2,连接DC,过点D作DE⊥DC交OA于点E.