Question

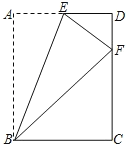
【题目】如图，矩形ABCD的边BC和AB的长分别为4和5，把它的左上角如图所示折叠．点A恰好落在CD边上的点F处，折痕为BE，则DE的长为(　　)

A.B.C.D.

Answer 1

【答案】A

【解析】

根据折叠的性质可得BF=AB，EF=AE，在Rt△BFC中根据勾股定理求出CF，从而求出DF，在Rt△DEF中根据勾股定理即可求得EF=AE，从而求得DE．

解：∵四边形ABCD是矩形，

∴AB=CD=5，AD=BC=4．

∵把它的左上角如图所示折叠．点A恰好落在CD边上的点F处，折痕为BE，

∴AE=EF，BF=AB=5，

∴CF3，

∴DF=5﹣3=2．

∵DE2+DF2=EF2，

∴(4﹣EF)2+22=EF2，

∴EF，

∴DE=AD﹣AE=AD﹣EF．

故选：A．