题目内容
甲、乙两人分别计算(3x+a)(4x+b).甲抄错a的符号,得到结果是12x2+17x+6,乙漏抄第二个括号中x的系数,得到结果是3x2+7x-6,问:
(1)a,b分别是多少?
(2)该题的正确答案是多少?
(1)a,b分别是多少?
(2)该题的正确答案是多少?
分析:(1)根据题意得出方程3b+a=7,3b-4a=17,组成方程组求出即可;
(2)把a、b的值代入,再根据多项式乘以多项式法则求出即可.
(2)把a、b的值代入,再根据多项式乘以多项式法则求出即可.
解答:解:(1)∵乙漏抄第二个括号中x的系数,得到结果是3x2+7x-6,
∴(3x+a)(x+b)=3x2+7x-6,
即3x2+3bx+ax+ab=3x2+(3b+a)x+ab=3x2+7x-6,
∴3b+a=7,
∵甲抄错a的符号,得到结果是12x2+17x+6,
∴(3x-a)(4x+b)=12x2+17x+6,
即12x2+3bx-4ax-ab=12x2+(3b-4a)x-ab=12x2+17x+6,
∴3b-4a=17,
即
解得:a=-2,b=3.
(2)(3x+a)(4x+b)
=(3x-2)(4x+3)
=12x2+9x-8x-6
=12x2+x-6.
∴(3x+a)(x+b)=3x2+7x-6,
即3x2+3bx+ax+ab=3x2+(3b+a)x+ab=3x2+7x-6,
∴3b+a=7,
∵甲抄错a的符号,得到结果是12x2+17x+6,
∴(3x-a)(4x+b)=12x2+17x+6,
即12x2+3bx-4ax-ab=12x2+(3b-4a)x-ab=12x2+17x+6,
∴3b-4a=17,
即
|
解得:a=-2,b=3.
(2)(3x+a)(4x+b)
=(3x-2)(4x+3)
=12x2+9x-8x-6
=12x2+x-6.
点评:本题考查了解二元一次方程组,多项式乘以多项式的应用,注意:(a+b)(m+n)=am+an+bm+bn.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
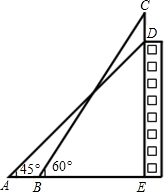 如图:某幢大楼顶部有一块广告牌CD,甲、乙两人分别在地面上相距12米的A、B两处测得点D和点C的仰角为45°和60°,且A、B、E三点在一条直线上,若BE=25m,求这块广告牌的高度.(取
如图:某幢大楼顶部有一块广告牌CD,甲、乙两人分别在地面上相距12米的A、B两处测得点D和点C的仰角为45°和60°,且A、B、E三点在一条直线上,若BE=25m,求这块广告牌的高度.(取 已知A地在B地正南方向3千米处,甲、乙两人分别从两地向正北方向匀速直行,他们与A地距离s(千米)与所行时间t(小时)之间的关系如图所示,其中l1表示甲运动的过程,l2表示乙运动的过程,根据图象回答:
已知A地在B地正南方向3千米处,甲、乙两人分别从两地向正北方向匀速直行,他们与A地距离s(千米)与所行时间t(小时)之间的关系如图所示,其中l1表示甲运动的过程,l2表示乙运动的过程,根据图象回答: 已知A地在B地正南方向3千米处,甲、乙两人分别从两地向正北方向匀速直行,他们与A地距离s(千米)与所行时间t(小时)之间的关系如图所示,其中l1表示甲运动的过程,l2表示乙运动的过程,根据图象回答:
已知A地在B地正南方向3千米处,甲、乙两人分别从两地向正北方向匀速直行,他们与A地距离s(千米)与所行时间t(小时)之间的关系如图所示,其中l1表示甲运动的过程,l2表示乙运动的过程,根据图象回答: ≈1.73,计算结果保留整数)
≈1.73,计算结果保留整数)