题目内容
如图,△OAB是边长为2的等边三角形,过点A的直线 +m与x轴交于点E.
+m与x轴交于点E.(1)求点E的坐标;
(2)求过A、O、E三点的抛物线解析式;
(3)若点P是(2)中求出的抛物线AE段上一动点(不与A、E重合),设四边形OAPE的面积为S,求S的最大值.

【答案】分析:(1)(2)由图可作AF⊥x轴于F,根据直角三角形性质,用待定系数求E点坐标和的抛物线解析式;
(3)再作作PG⊥x轴于G,将四边形OAPE的面积S用x来表示,将问题转化为求函数最值问题.
解答: 解:(1)作AF⊥x轴于F,
解:(1)作AF⊥x轴于F,
∴OF=OAcos60°=1,AF=OFtan60°=
∴点A(1, )(1分)
)(1分)
代入直线解析式,
得 ,
,
∴m=
∴
当y=0时,
得x=4,∴点E(4,0)(3分)
(2)设过A、O、E三点抛物线的解析式为y=ax2+bx+c
∵抛物线过原点
∴c=0
 ,
,
∴
∴抛物线的解析式为 (6分)
(6分)

(3)作PG⊥x轴于G,设P(x,y)
S四边形OAPE=S△AOF+S梯形AFGP+S△PGE
= (8分)
(8分)
=
当 时,S最大=
时,S最大= .(10分)
.(10分)
点评:此题考查知识点多,但题难度不大,需作辅多条辅助线,在直角三角形中解题,将问题转化为求函数最值问题.
(3)再作作PG⊥x轴于G,将四边形OAPE的面积S用x来表示,将问题转化为求函数最值问题.
解答:
 解:(1)作AF⊥x轴于F,
解:(1)作AF⊥x轴于F,∴OF=OAcos60°=1,AF=OFtan60°=

∴点A(1,
 )(1分)
)(1分)代入直线解析式,
得
 ,
,∴m=

∴

当y=0时,

得x=4,∴点E(4,0)(3分)
(2)设过A、O、E三点抛物线的解析式为y=ax2+bx+c
∵抛物线过原点
∴c=0
 ,
,∴

∴抛物线的解析式为
 (6分)
(6分)
(3)作PG⊥x轴于G,设P(x,y)
S四边形OAPE=S△AOF+S梯形AFGP+S△PGE
=
 (8分)
(8分)=

当
 时,S最大=
时,S最大= .(10分)
.(10分)点评:此题考查知识点多,但题难度不大,需作辅多条辅助线,在直角三角形中解题,将问题转化为求函数最值问题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
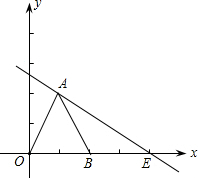 如图,△OAB是边长为2的等边三角形,过点A的直线
如图,△OAB是边长为2的等边三角形,过点A的直线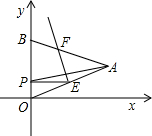 OAB折叠,使点A与OB边上的点P重合,折痕与OA、AB的交点分别是E、F.如果PE∥x轴,
OAB折叠,使点A与OB边上的点P重合,折痕与OA、AB的交点分别是E、F.如果PE∥x轴,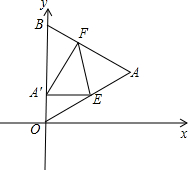 若能,请求出此时点A′的坐标;若不能,请你说明理由.
若能,请求出此时点A′的坐标;若不能,请你说明理由. 如图,△OAB是边长为
如图,△OAB是边长为 OAB 折叠,使点A落在边OB上,记为A′,折痕为EF.
OAB 折叠,使点A落在边OB上,记为A′,折痕为EF.