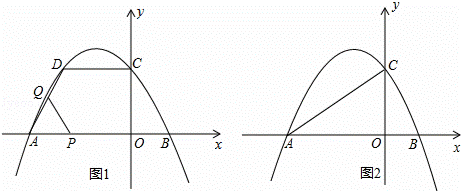题目内容
如图，在△ABC中，以AB为直径的⊙O交AC于点D，过点D作DE⊥BC于点E，且∠BDE=∠A．
（1）判断DE与⊙O的位置关系并说明理由；
（2）若AC=16，tanA=
，求⊙O的半径．
解：（1）DE与⊙O相切．理由如下：
连接DO，BD，如图，
∵∠BDE=∠A，∠A=∠ADO，
∴∠ADO=∠EDB，
∵AB为⊙O的直径，
∴∠ADB=90°，
∴∠ADO+∠ODB=90°，
∴∠ODB+∠EDB=90°，即∠ODE=90°，
∴OD⊥DE，
∴DE为⊙O的切线；
（2）∵∠BDE=∠A，
∴∠ABD=∠EBD，
而BD⊥AC，
∴△ABC为等腰三角形，
∴AD=CD=
AC=8，
在Rt△ABD中，∵tanA=
=，
∴BD=×8=6，
∴AB=
=10，
∴⊙O的半径为5．
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
B．
C．
D．
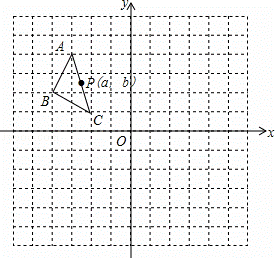
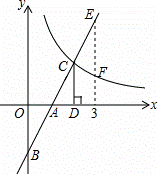
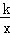（x＞0）交于点C，过点C作CD⊥x轴，垂足为D，且OA=AD，则以下结论：
；
）
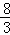，其中a=﹣3．
B． 
C． 
D． 
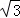与x轴交于A（﹣3，0），B（1，0）两点．与y轴交于点C，点D与点C关于抛物线的对称轴对称．
过程中，△APQ与四边形AOCD重叠部分的面积为S，点P的运动时间为t秒，求S与t之间的函数关系式；