Question

【题目】已知二次函数（、为常数）的图像经过点和点.

（1）求、的值；

（2）如图1，点在抛物线上，点是轴上的一个动点，过点平行于轴的直线平分，求点的坐标；

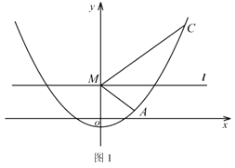
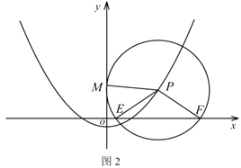
（3）如图2，在（2）的条件下，点是抛物线上的一动点，以为圆心、为半径的圆与轴相交于、两点，若的面积为，请直接写出点的坐标.

Answer 1

【答案】（1），；（2）；（3）或或

【解析】

(1)直接把两点的坐标代入二次函数解析式，得出关于b，c的二元一次方程组求解即可

(2) 过点作，过点作.证明△CMD相似于△AME，再根据对应线段成比例求解即可

(3)根据题意设点P的纵坐标为y，首先根据三角形面积得出EF与y的关系，再利用勾股定理得出EF与y的关系，从而得出y的值，再代入抛物线解析式求出x的值，得出点坐标.

解：(1)把和代入得：

解方程组得出：

所以，

，

(2)由已知条件得出C点坐标为，设.过点作，过点作.

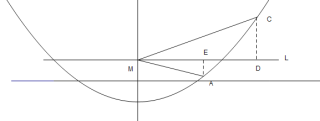
两个直角三角形的三个角对应相等，

∴

∴

∴

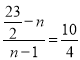
∵解得：

∴

(3)设点P的纵坐标为y,由题意得出，，

∵MP与PE都为圆的半径，

∴MP=PE

∴

整理得出，

∴

∵

∴y=1,

∴当y=1时有，，解得，；

∴当y=-1时有，，此时，x=0

∴综上所述得出P的坐标为：或或