题目内容
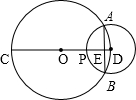如图，CD是⊙O的直径，以D为圆心的圆与⊙O交于A、B两点，AB交CD于点E，CD交⊙D于P，已知PC=6，PE：ED=2：1，则AB的长为（ ）A、6
| ||
B、4
| ||
C、2
| ||
D、
|
分析：延长PD交⊙D于F．设PE=2x，DE=x，根据相交两圆的性质，知AE=BE．根据相交弦定理列方程求解．
解答：
解：延长PD交⊙D于F．
设PE=2x，DE=x．
根据相交弦定理，得：
CE×ED=AE×BE=PE×EF，
（6+2x）×x=2x×4x，
解得x=1．
所以AE=BE=2
，
所以AB=4
．
故选B．
解：延长PD交⊙D于F．设PE=2x，DE=x．
根据相交弦定理，得：
CE×ED=AE×BE=PE×EF，
（6+2x）×x=2x×4x，
解得x=1．
所以AE=BE=2
| 2 |
所以AB=4
| 2 |
故选B．
点评：此题综合运用了相交弦定理和相交两圆的性质．
练习册系列答案
阅读快车系列答案
相关题目
（2013•抚顺）在与水平面夹角是30°的斜坡的顶部，有一座竖直的古塔，如图是平面图，斜坡的顶部CD是水平的，在阳光的照射下，古塔AB在斜坡上的影长DE为18米，斜坡顶部的影长DB为6米，光线AE与斜坡的夹角为30°，求古塔的高（
如图，某水库堤坝的横断面为梯形，背水坡AD的坡比（坡比是斜坡的铅直距离与水平距离的比）为1：1.5，迎水坡BC的坡比为1：