题目内容
14.等边三角形的边长是6,它的高等于3$\sqrt{3}$,面积等于9$\sqrt{3}$.分析 根据等边三角形三线合一的性质可得D为BC的中点,即BD=CD,在直角三角形ABD中,已知AB、BD,根据勾股定理即可求得AD的长,即可求三角形ABC的面积,即可解题.
解答 解:等边三角形高线即中线,故D为BC中点,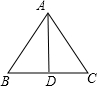
∵AB=6,
∴BD=3,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}=3\sqrt{3}$,
∴等边△ABC的面积=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×6×3$\sqrt{3}$=9$\sqrt{3}$.
故答案为:3$\sqrt{3}$,9$\sqrt{3}$.
点评 本题考查了勾股定理在直角三角形中的运用,等边三角形面积的计算,本题中根据勾股定理计算AD的值是解题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
9. 如图,直线AB与CD相交于点O,过点O作OE⊥AB,若∠1=35°,则∠2的度数是( )
如图,直线AB与CD相交于点O,过点O作OE⊥AB,若∠1=35°,则∠2的度数是( )
 如图,直线AB与CD相交于点O,过点O作OE⊥AB,若∠1=35°,则∠2的度数是( )
如图,直线AB与CD相交于点O,过点O作OE⊥AB,若∠1=35°,则∠2的度数是( )| A. | 45° | B. | 55° | C. | 65° | D. | 75° |
19.已知n是正整数,且$\sqrt{45n}$也是一个正整数,则正整数n的最小值为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 9 |
6.计算25m÷5m的结果为( )
| A. | 5 | B. | 5m | C. | 20 | D. | 20m |
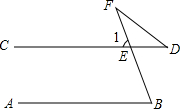 如图,AB∥CD,∠B=78°,∠D=32°,求∠F的度数.
如图,AB∥CD,∠B=78°,∠D=32°,求∠F的度数. 如图,边长等于4的正方形ABCD两个顶点A与D分别在x轴和y轴上滑动(A、D都不与坐标原点O重合),作CE⊥x轴,垂足为E,当OA等于2$\sqrt{2}$时,四边形OACE面积最大.
如图,边长等于4的正方形ABCD两个顶点A与D分别在x轴和y轴上滑动(A、D都不与坐标原点O重合),作CE⊥x轴,垂足为E,当OA等于2$\sqrt{2}$时,四边形OACE面积最大.