题目内容
如图,点B、C、D都在⊙O上,过C点作CA∥BD,交OD的延长线于点A,连接BC,∠B=∠A=30º,BD= 。
。

(1)求证:AC是⊙O的切线。
(2)求由线段AC、AD与弧CD所围成的阴影部分的面积(结果保留π)。
(1)证明见解析;(2)2 ﹣
﹣ .
.
【解析】
试题分析:(1)连接OC,根据圆周角定理求出∠COA,根据三角形内角和定理求出∠OCA,根据切线的判定推出即可;
(2)求出DE,解直角三角形求出OC,分别求出△ACO的面积和扇形COD的面积,即可得出答案.
试题解析:(1)证明:连接OC,交BD于E,
∵∠B=30°,∠B= ∠COD,
∠COD,
∴∠COD=60°,
∵∠A=30°,
∴∠OCA=90°,
即OC⊥AC,
∴AC是⊙O的切线;
(2)【解析】
∵AC∥BD,∠OCA=90°,
∴∠OED=∠OCA=90°,
∴DE= BD=
BD= ,
,
∵sin∠COD= ,
,
∴OD=2,
在Rt△ACO中,tan∠COA= ,
,
∴AC=2 ,
,
∴S阴影= ×2×2
×2×2 ﹣
﹣ =2
=2 ﹣
﹣ .
.

考点:1.切线的判定;2.扇形面积的计算.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 的图象先沿
的图象先沿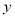 轴向上平移3个单位,再沿
轴向上平移3个单位,再沿 轴向右平移2个单位后得到的图象对应的函数关系式为 .
轴向右平移2个单位后得到的图象对应的函数关系式为 .
 (k<0)图像的两支分别在( )
(k<0)图像的两支分别在( )
