题目内容
探索发现:
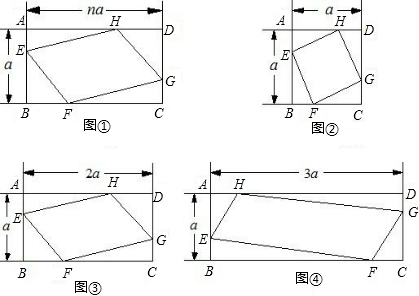
已知矩形ABCD的面积是10,P是AD边所在直线上一点
(1)如图1,当点P与点D重合时,S△PBC=
(2)如图2,当点P是AD边上不与A、D两点重合的一点时,S△PBC=
(3)如图3,当点P是AD(或DA)延长线上一点时,S△PBC=
联系拓展:
如图4,矩形ANCD的面积是10,E、F分别是BC边和DC边延长线上的点,连接EA、ED、FA、FB,求图中阴影部分的面积,并简要说明理由.
解决问题:
如图5,矩形ABCD中,EF与GH交于点O,EF与CH把矩形分成四个区域,其中SAEOG=700m2,SEBHO=600m2,SOHCF=500m2,求图中阴影部分的面积.

已知矩形ABCD的面积是10,P是AD边所在直线上一点
(1)如图1,当点P与点D重合时,S△PBC=
5
5
;(2)如图2,当点P是AD边上不与A、D两点重合的一点时,S△PBC=
5
5
;(3)如图3,当点P是AD(或DA)延长线上一点时,S△PBC=
5
5
.联系拓展:
如图4,矩形ANCD的面积是10,E、F分别是BC边和DC边延长线上的点,连接EA、ED、FA、FB,求图中阴影部分的面积,并简要说明理由.
解决问题:
如图5,矩形ABCD中,EF与GH交于点O,EF与CH把矩形分成四个区域,其中SAEOG=700m2,SEBHO=600m2,SOHCF=500m2,求图中阴影部分的面积.

分析:(1)直接根据S△PBC=
BC×CD求出即可;
(2)直接根据S△PBC=
BC×PM求出即可;
(3)直接根据S△PBC=
BC×PM求出即可;图4,过E作EN⊥AD交AD延长线于N,过F作FQ⊥AB交AB延长线于Q,则阴影部分的面积S=S△EAD+S△FAB,图5中,阴影部分的面积:S=S△DEO+S△DOH+S△EOH,进而得出答案.
| 1 |
| 2 |
(2)直接根据S△PBC=
| 1 |
| 2 |
(3)直接根据S△PBC=
| 1 |
| 2 |
解答: 解:(1)∵矩形ABCD的面积是10,
解:(1)∵矩形ABCD的面积是10,
∴BC×CD=10,
∴S△PBC=
BC×CD=
×10=5,
故答案为:5.
(2)过P作PM⊥BC于M,
∵四边形ABCD是矩形,
∴AB=CD,∠A=∠ABM=∠PMB=90°,
∴四边形ABMP是矩形,
∴PM=AB=CD,
图2中S△PBC=
BC×PM=
BC×DC=
×10=5,
故答案为:5.
(3)过P作PM⊥BC于M,
∵四边形ABCD是矩形,
∴AB=CD,∠A=∠ABM=∠PMB=90°,
∴四边形ABMP是矩形,
∴PM=AB=CD,
图2中S△PBC=
BC×PM=
BC×DC=
×10=5,
图4,过E作EN⊥AD交AD延长线于N,过F作FQ⊥AB交AB延长线于Q,
则NE=CD,FQ=BC,
则阴影部分的面积S=S△EAD+S△FAB=
AD×EN+
AB×FQ=
BC×CD+
CD×BC=
×10+
×10=10.
图5中,
阴影部分的面积:
S=S△DEO+S△DOH+S△EOH
=
S四边形AEOG+
S四边形OHCF+
S四边形EBHO
=
×700+
×600+
×500
=900.
故答案为:5.
 解:(1)∵矩形ABCD的面积是10,
解:(1)∵矩形ABCD的面积是10,∴BC×CD=10,
∴S△PBC=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:5.
(2)过P作PM⊥BC于M,
∵四边形ABCD是矩形,
∴AB=CD,∠A=∠ABM=∠PMB=90°,
∴四边形ABMP是矩形,
∴PM=AB=CD,
图2中S△PBC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:5.
(3)过P作PM⊥BC于M,
∵四边形ABCD是矩形,
∴AB=CD,∠A=∠ABM=∠PMB=90°,
∴四边形ABMP是矩形,
∴PM=AB=CD,
图2中S△PBC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
图4,过E作EN⊥AD交AD延长线于N,过F作FQ⊥AB交AB延长线于Q,
则NE=CD,FQ=BC,
则阴影部分的面积S=S△EAD+S△FAB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
图5中,
阴影部分的面积:
S=S△DEO+S△DOH+S△EOH
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=900.
故答案为:5.
点评:此题主要考查了三角形面积求法以及利用分割法求出图形面积,根据已知得出矩形面积与三角形面积的关系是解题关键.

练习册系列答案
相关题目

 证)
证)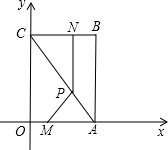 如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(6,0),(6,8).动点M、N分别从O、B同时出发,以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点N作NP⊥BC,交AC于P,连接MP.已知动点运动了x秒.
如图,平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(6,0),(6,8).动点M、N分别从O、B同时出发,以每秒1个单位的速度运动.其中,点M沿OA向终点A运动,点N沿BC向终点C运动.过点N作NP⊥BC,交AC于P,连接MP.已知动点运动了x秒.