题目内容
7.如图，在△ABC中，BA=BC，∠B=120°，AB的垂直平分线交AC与D.求证：AD=1/2DC.
分析：连接BD，根据线段垂直平分线上的点到线段两端点的距离相等可得AD=BD，然后求出∠A=∠C=∠ABD=30°，再求出∠DBC=90°，再根据直角三角形30°所对的直角边等于斜边的一半即可得证．解答：解：如图，连接DB．
∵AB被垂直平分，
∴AD=DB，
∴∠A=∠ABD，
∵BA=BC，∠B=120°，
∴∠A=∠C=
（180°-120°）=30°，
∴∠ABD=30°，
又∵∠ABC=120°，
∴∠DBC=120°-30°=90°，
∴BD=
DC，
∴AD=
DC．
∵AB被垂直平分，
∴AD=DB，
∴∠A=∠ABD，
∵BA=BC，∠B=120°，
∴∠A=∠C=
| 1 |
| 2 |
∴∠ABD=30°，
又∵∠ABC=120°，
∴∠DBC=120°-30°=90°，
∴BD=
| 1 |
| 2 |
∴AD=
| 1 |
| 2 |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
，当x=-2时，y=5，求当x=2时，y的值。
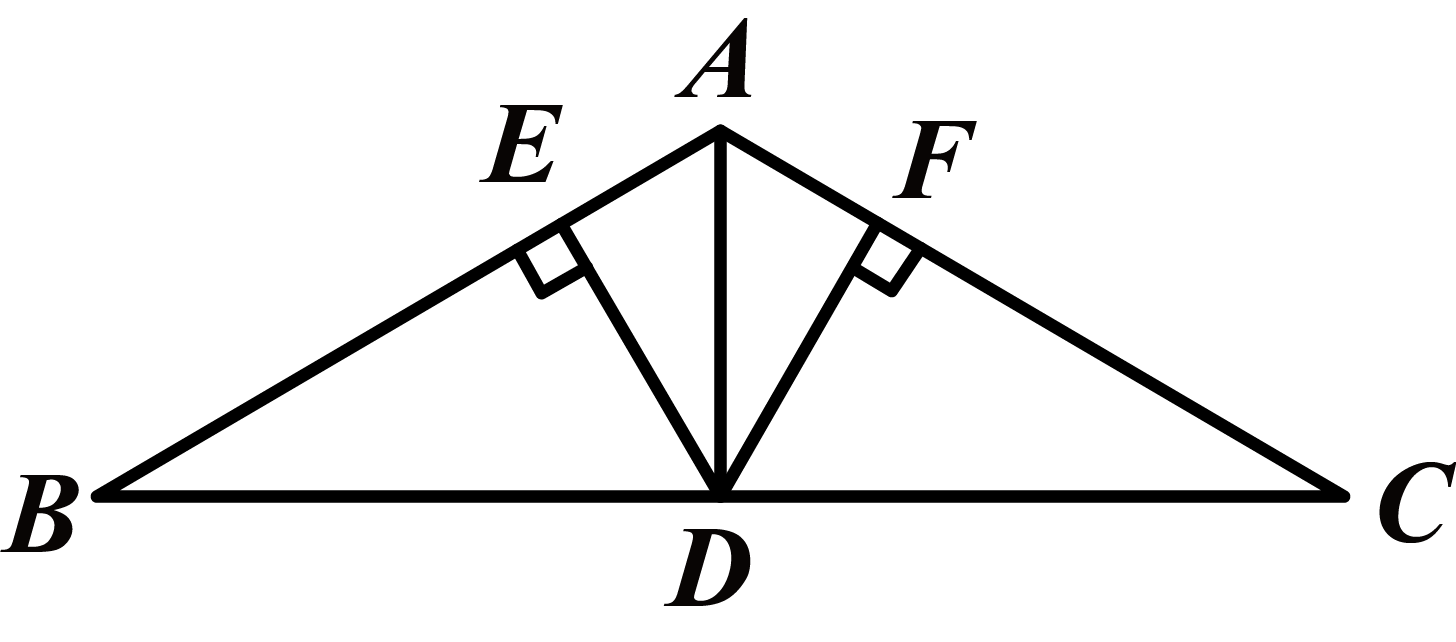3.如图所示的是屋顶的“人字形”钢架，其中斜梁AB＝AC，顶角∠BAC＝120°，跨度BC＝10 m，AD为柱（即底边BC的中线），两根支撑架DE⊥AB，DF⊥AC，则DE＋DF＝________．