题目内容
【题目】在平面直角坐标系
中，抛物线
与
轴交于点
．
（1）求点的坐标（用含
的式子表示）；
（2）求抛物线的对称轴；
（3）已知点
．若抛物线与线段
恰有一个公共点，结合函数图象，求的取值范围．
【答案】（1）
；（2）
；（3）
的取值范围是
【解析】
（1）与
轴的交点横坐标为0，然后计算
时的函数值即可求出坐标；
（2）根据抛物线的对称轴为
求解即可；
（3）由N点和A点的坐标，可知点A在点N的上方，令抛物线上的点
，可得
，分a＞0，a＜0两种情形分别求解即可解决问题．
解：（1）∵抛物线
与轴交于点
，
令，得
．
．
（2）由抛物线可知
．
∴抛物线的对称轴为直线．
（3）对于任意的实数，都有
．
可知点总在点
的上方．
令抛物线上的点．
．
①如图1，当
时， 
．
∴点
在点
的上方．
结合函数图象，可知抛物线与线段
没有公共点．
②当
时
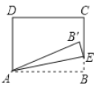
（i）如图2，当抛物线经过点时， 
．
．
结合函数图象，可知抛物线与线段恰有一个公共点．
（ii）当
时，可知抛物线与线段没有公共点．
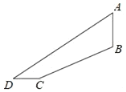
（ⅲ）如图3，当
，时， 
．
∴点在点的下方．
结合函数图象，可知抛物线与线段恰有一个公共点．
综上所述， 的取值范围是．
【题目】如图，点C是以点O为圆心，AB为直径的半圆上的动点（不与点A，B重合），AB＝6cm，过点C作CD⊥AB于点D，E是CD的中点，连接AE并延长交
于点F，连接FD．小腾根据学习函数的经验，对线段AC，CD，FD的长度之间的关系进行了探究．
下面是小腾的探究过程，请补充完整：
（1）对于点C在上的不同位置，画图、测量，得到了线段AC，CD，FD的长度的几组值，如表：
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | |
AC/cm | 0.1 | 0.5 | 1.0 | 1.9 | 2.6 | 3.2 | 4.2 | 4.9 |
CD/cm | 0.1 | 0.5 | 1.0 | 1.8 | 2.2 | 2.5 | 2.3 | 1.0 |
FD/cm | 0.2 | 1.0 | 1.8 | 2.8 | 3.0 | 2.7 | 1.8 | 0.5 |
在AC，CD，FD的长度这三个量中，确定 的长度是自变量， 的长度和 的长度都是这个自变量的函数；
（2）在同一平面直角坐标系xOy中，画出（1）中所确定的函数的图象；
（3）结合函数图象，解答问题：当CD＞DF时，AC的长度的取值范围是 ．
