题目内容
13.在平面直角坐标系中,A点为直线y=x上的一点,过A点作AB⊥x轴于点B,OB=4,E是OB边上的一点,且OE=3,点P为线段AO上的动点,则△BEP周长最小值为6.分析 作AC⊥y轴于C,连接CE,交OA于P,此时PB+PE=CE,根据两点之间线段最短,则此时△BEP周长最小.求得四边形ABOC是正方形,从而得出C关于直线y=x对称,然后根据勾股定理求得CE,即可求得△BEP周长最小值.
解答 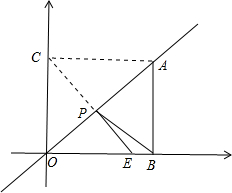 解:如图,作AC⊥y轴于C,连接CE,交OA于P,此时PB+PE=CE,根据两点之间线段最短,则此时△BEP周长最小,
解:如图,作AC⊥y轴于C,连接CE,交OA于P,此时PB+PE=CE,根据两点之间线段最短,则此时△BEP周长最小,
∵A点为直线y=x上的一点,OB=4,
∴A(4,4),
∴AC=OC=4,
∴四边形ABOC是正方形,
∴C关于直线y=x对称,
∵OC=4,OE=3,
∴CE=5,
∴PB+PE的最小值为5,
∵BE=1,
∴△BEP周长最小值为5+1=6;
故答案为6.
点评 本题考查了正方形的性质、轴对称的性质以及勾股定理等知识的综合应用,解题的难点在于确定满足条件的点P的位置:利用轴对称的方法.然后熟练运用勾股定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
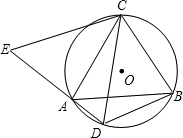 如图所示,△ABC是⊙O的内接三角形,AC=BC,D为⊙O中弧AB上一点,延长DA至点E,使CE=CD.
如图所示,△ABC是⊙O的内接三角形,AC=BC,D为⊙O中弧AB上一点,延长DA至点E,使CE=CD.
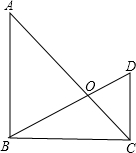 如图,已知△ABC和△BCD都是直角三角形,AB⊥BC,CD⊥BC,∠A=45°,∠D=60°,AC与BD交于点O,求∠BOC的度数.
如图,已知△ABC和△BCD都是直角三角形,AB⊥BC,CD⊥BC,∠A=45°,∠D=60°,AC与BD交于点O,求∠BOC的度数.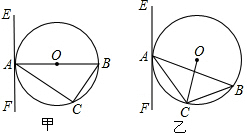
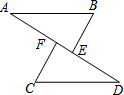 如图,AB∥CD,AB=CD,点E、F在AD上,且AE=DF.
如图,AB∥CD,AB=CD,点E、F在AD上,且AE=DF.