题目内容
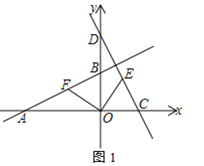
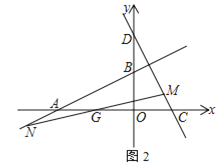
【题目】如图,直线y=![]() x+2与x轴交于点A,与y轴交于点B,抛物线y=﹣
x+2与x轴交于点A,与y轴交于点B,抛物线y=﹣![]() x2+bx+c经过A、B两点,与x轴的另一个交点为 C.
x2+bx+c经过A、B两点,与x轴的另一个交点为 C.
(1)求抛物线的解析式;
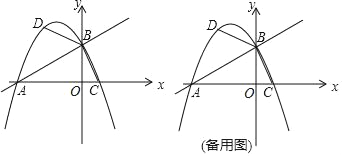
(2)直线AB上方抛物线上的点D,使得∠DBA=2∠BAC,求D点的坐标;
(3)M是平面内一点,将△BOC绕点M逆时针旋转90°后,得到△B1O1C1,若△B1O1C1的两个顶点恰好落在抛物线上,请求点B1的坐标.
【答案】(1)y=﹣![]() x2﹣
x2﹣![]() x+2;(2)D(﹣2,3);(3)B1的坐标为(﹣
x+2;(2)D(﹣2,3);(3)B1的坐标为(﹣![]() ,
,![]() )或(﹣3,2).
)或(﹣3,2).
【解析】
当x=0时,当y=0时求出A,B点在代入y=﹣![]() x2+bx+c,求出b,c,即可求解.
x2+bx+c,求出b,c,即可求解.
取点B关于x轴的对称点B′(0,﹣2),连接AB′,过点B作BD∥AB′交抛物线于点D,因为B、B′关于x轴对称,所以AB=AB′,∠BAB′=2∠BAC,设AB′:y=kx﹣2,代入A点求出k值,则![]() ,再由直线BD和抛物线交于点D列方程组求出,再根据象限即可求解.
,再由直线BD和抛物线交于点D列方程组求出,再根据象限即可求解.
因为△BOC绕点M逆时针旋转90°,所以![]() ∥x轴,
∥x轴,![]() ∥y轴,分类讨论当B1、O1在抛物线上时和当B1、C1在抛物线上时两种情况.
∥y轴,分类讨论当B1、O1在抛物线上时和当B1、C1在抛物线上时两种情况.
解:(1)y=![]() ,当x=0时,y=2;当y=0时,x=﹣4,
,当x=0时,y=2;当y=0时,x=﹣4,
∴A(﹣4,0),B(0,2),
把A、B的坐标代入y=﹣![]() x2+bx+c,得
x2+bx+c,得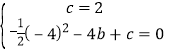 ,
,
解得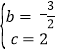 ,
,
∴抛物线的解析式为:y=﹣![]() x2﹣
x2﹣![]() x+2;
x+2;

(2)取点B关于x轴的对称点B′(0,﹣2),连接AB′,过点B作BD∥AB′交抛物线于点D,
∵B、B′关于x轴对称,
∴AB=AB′,∠BAB′=2∠BAC,
设AB′:y=kx﹣2,
代入A(﹣4,0)得﹣4k﹣2=0,解得k=﹣![]() ,
,
则BD:y=﹣![]() x+2,
x+2,
解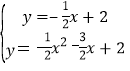 得
得![]() ,,
,,
∴D(﹣2,3).
(3)∵△BOC绕点M逆时针旋转90°,
∴B1O1∥x轴,O1C1∥y轴,
当B1、O1在抛物线上时,设B1的横坐标为x,则O1的横坐标为x+2,
∴﹣![]() x2﹣
x2﹣![]() x+2=﹣
x+2=﹣![]() (x+2)2﹣
(x+2)2﹣![]() (x+2)+2,
(x+2)+2,
解得x=﹣![]() ,
,
则B1(﹣![]() ,
,![]() );
);
当B1、C1在抛物线上时,设B1的横坐标为x,则C1的横坐标为x+2,
C1的纵坐标比B1的纵坐标大1,
∴﹣![]() x2﹣
x2﹣![]() x+2=﹣
x+2=﹣![]() (x+2)2﹣
(x+2)2﹣![]() (x+2)+2﹣1,解得x=﹣3,
(x+2)+2﹣1,解得x=﹣3,
则B1(﹣3,2),
∴B1的坐标为(﹣![]() ,
,![]() )或(﹣3,2).
)或(﹣3,2).