Question

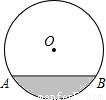
如图，水平放置的圆柱形排水管的截面为⊙O，有水部分弓形的高为2，弦AB=

（1）求⊙O的半径；

（2）求截面中有水部分弓形的面积．（保留根号及π）

Answer 1

考点：

垂径定理的应用；勾股定理．.

专题：

探究型．

分析：

（1）过点O作OC⊥AB于点D，交于点C，连接OB，设⊙O的半径为R，则OD=R﹣2，再根据垂径定理求出BD的长，由勾股定理即可得出R的值；

（2）连接OA，根据（1）中OB、BD的长求出∠BOD的度数，根据S_弓形=S_扇形ACB﹣S_△AOB即可得出结论．

解答：

解：（1）过点O作OC⊥AB于点D，交于点C，连接OB，设⊙O的半径为r，则OD=r﹣2，

∵OC⊥AB，

∴BD=AB=×4=2，

在Rt△BOD中，

∵OD²+BD²=OB²，即（r﹣2）²+（2）²=r²，解得r=4；

（2）∵由（1）可知，BD=2，OB=4，

∴sin∠BOD===，

∴∠BOD=60°，

∴∠AOB=2∠BOD=120°，

∴S_弓形=S_扇形AOB﹣S_△AOB=﹣×2×2=﹣2．

点评：

本题考查的是垂径定理的应用，根据题意作出辅助线，利用垂径定理求解是解答此题的关键．