Question

4．如图，以AC为直径的⊙O与BC相切于点C，连接AB交⊙O于点D，过点D作⊙O的切线，交BC于E
（1）若∠ACD=20°，求∠DEC的大小
（2）当以点O、D、E、C为顶点的四边形是正方形时，求∠ABC的大小．

Answer 1

分析 （1）连接OD，根据AC是⊙O的直径，DE，BC是⊙O的切线，推出∠EDO∠ACE=90°，由OD=OC，得到∠ODC=∠OCD=20°，关键四边形的内角和=360°解出结果；
（2）由四边形ODEC是正方形，得到DE=CE，∠DEC=90°，由等腰直角三角形的性质得到∠DCE=45°，由AC是⊙O的直径，得出∠BDC=∠ADC=90°，解得∠ABC=45°．

解答 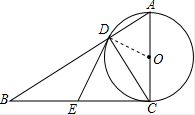解：（1）连接OD，
∵AC是⊙O的直径，DE，BC是⊙O的切线，
∴∠EDO∠ACE=90°，
∵OD=OC，
∴∠ODC=∠OCD=20°，
∴∠DOC=140，
∴∠DEC=40°；

（2）∵四边形ODEC是正方形，
∴DE=CE，∠DEC=90°，
∴∠DCE=45°，
∵AC是⊙O的直径，
∴∠BDC=∠ADC=90°，
∴∠ABC=45°．

点评 本题考查了切线的性质，圆周角定理，正方形的性质，正确的作出辅助线是解题的关键．