题目内容
20. 如图,CD为△ABC的角平分线.E、F分别在CD、BD上.且DA=DF,EF=AC,
如图,CD为△ABC的角平分线.E、F分别在CD、BD上.且DA=DF,EF=AC,求证:EF∥BC.
分析 延长ED到G,使ED=DG,连结AG,可证△AGD与△FED全等,利用全等三角形的性质证明即可.
解答 证明:延长ED到G,使ED=DG,连结AG,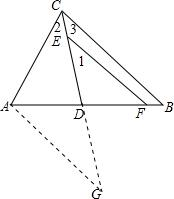
在△AGD与△FED中,
$\left\{\begin{array}{l}{AD=FD}\\{∠ADG=∠FDE}\\{ED=GD}\end{array}\right.$,
∴△AGD≌△FED(SAS),
∴∠1=∠G,AG=EF,
∵EF=AC,
∴AC=AG,
∴∠2=∠G,
∵∠2=∠3,∠G=∠1,
∴∠3=∠1,
∴EF∥BC.
点评 此题考查全等三角形的判定和性质,关键是证△AGD与△FED全等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.下列函数中,自变量x的取值范围是x>-2的是( )
| A. | y=x+2 | B. | y=$\frac{1}{x+2}$ | C. | y=$\sqrt{x+2}$ | D. | y=$\frac{x-2}{\sqrt{x+2}}$ |
9.计算$\root{3}{27}$的结果是( )
| A. | ±3 | B. | 3 | C. | 3$\sqrt{3}$ | D. | $\sqrt{3}$ |
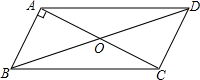 如图,平行四边形ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$,则BD=2$\sqrt{2}$.
如图,平行四边形ABCD中,AB⊥AC,AB=1,BC=$\sqrt{5}$,则BD=2$\sqrt{2}$. 如图,已知点O在直线AB上,OD平分∠AOC,OE平分∠BOC,求∠DOE的度数.
如图,已知点O在直线AB上,OD平分∠AOC,OE平分∠BOC,求∠DOE的度数.