题目内容
2. 如图,在△ABC中,AB=AC,AD⊥BC,BE⊥AC,则下列结论不正确的是( )
如图,在△ABC中,AB=AC,AD⊥BC,BE⊥AC,则下列结论不正确的是( )| A. | BD=DC | B. | CE=AE | C. | ∠BAD=∠CAD | D. | ∠CBE=∠DAC |
分析 根据等腰三角形的性质得到BD=CD,∠BAD=∠CAD,故①③正确;根据垂直的定义得到∠ADC=∠BEC=90°,根据三角形的内角和得到∠CBE=∠DAC,故④正确;由AB≠BC,AD⊥BC,得到CE≠AE.故③错误.
解答 解:∵AB=AC,AD⊥BC,
∴BD=CD,∠BAD=∠CAD,故①③正确;
∵AD⊥BC,BE⊥AC,
∴∠ADC=∠BEC=90°,
∴∠CBE=90°-∠C,∠DAC=90°-∠C,
∴∠CBE=∠DAC,故④正确;
∵AB≠BC,AD⊥BC,
∴CE≠AE,
故选B.
点评 本题考查了等腰三角形的性质,熟记等腰三角形的性质是解题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
13.下列事件为必然事件的是( )
| A. | 任意掷一枚均匀的硬币,正面朝上 | B. | 篮球运动员投篮,投进篮筐 | ||
| C. | 一个星期有七天 | D. | 打开电视机,正在播放新闻 |
7.若a<0,下列式子正确的是( )
| A. | -a<0 | B. | a2>0 | C. | a2=-a2 | D. | a3=-a3 |
14.下列几何图形不一定是轴对称图形的是( )
| A. | 角 | B. | 等边三角形 | C. | 等腰三角形 | D. | 直角三角形 |
11.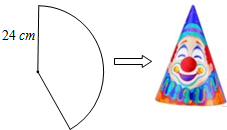 小洋用一张半径为24cm的扇形纸板做一个如图所示的圆锥形小丑帽子侧面(接缝忽略不计),如果做成的圆锥形小丑帽子的底面半径为10cm,那么这张扇形纸板的面积是( )
小洋用一张半径为24cm的扇形纸板做一个如图所示的圆锥形小丑帽子侧面(接缝忽略不计),如果做成的圆锥形小丑帽子的底面半径为10cm,那么这张扇形纸板的面积是( )
 小洋用一张半径为24cm的扇形纸板做一个如图所示的圆锥形小丑帽子侧面(接缝忽略不计),如果做成的圆锥形小丑帽子的底面半径为10cm,那么这张扇形纸板的面积是( )
小洋用一张半径为24cm的扇形纸板做一个如图所示的圆锥形小丑帽子侧面(接缝忽略不计),如果做成的圆锥形小丑帽子的底面半径为10cm,那么这张扇形纸板的面积是( )| A. | 120πcm2 | B. | 240πcm2 | C. | 260πcm2 | D. | 480πcm2 |
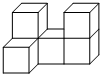 如图所示的几何体是由形状、大小都完全相同的小正方体组合而成的,则下列图形不可能是它的三视图的是( )
如图所示的几何体是由形状、大小都完全相同的小正方体组合而成的,则下列图形不可能是它的三视图的是( )